
Техника интегрирования
Теорема, доказанная на стр. 473, сводит проблему интегрирования функции f(x) в пределах от а до b к нахождению функции G(x), первообразной по отношению к функции f(х). Интеграл тогда просто равен разности G(b)-G(b).
Для таких первообразных функций (определяемых с точностью до постоянного слагаемого) употребительно наименование "неопределенный интеграл" и чрезвычайно удобное обозначение
G(x) = ∫ f(x)dx,
без обозначения пределов интегрирования. (Это обозначение может несколько дезориентировать начинающего: см. замечания на стр. 473.)
Из каждой формулы дифференцирования легко получить, путем ее обращения, некоторую формулу неопределенного интегрирования. К этой, несколько эмпирической, процедуре мы здесь добавим два важных правила, которые по существу представляют собой не что иное, как обращение правил дифференцирования сложной функции и произведения двух функций. В их интегральной форме их называют правилами интегрирования посредством подстановки и интегрирования "по частям".
А) Первое правило вытекает из формулы дифференцирования сложной функции
Н (u) = G(x),
где функции
х = ψ(u) и u = φ(х)
предполагаются взаимно однозначно связанными в рассматриваемой области.
В таком случае мы имеем:
H'(u) = G'(x)ψ'(u).
Полагая
G'(x) = f(x),
мы можем написать
G (х) = ∫ f (х) dx
и также
G'(x)ψ'(u) = f(x)ψ'(u),
а это вследствие предыдущей формулы для Н'(u) равносильно
Н (u) = &38747; f[ψ(u)]ψ'(u)] du.
Итак, принимая во внимание, что H (u) = G (x), мы получаем:
∫ f(x) dx = ∫f[ψ(u)]ψ'(u)du. (I)
Будучи записано в обозначениях Лейбница (см. стр. 468), это правило принимает практически очень удобный вид
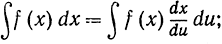
оказывается, что мы не сделаем ошибки, если символ dx заменим символом 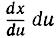 так, как будто бы dx и du были числами, а
так, как будто бы dx и du были числами, а 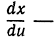 их отношением.
их отношением.
Проиллюстрируем полезность формулы (I) несколькими примерами.
a) 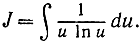 Станем читать формулу (I) справа налево, полагая в ней х = ln u = ψ(u). Тогда получим
Станем читать формулу (I) справа налево, полагая в ней х = ln u = ψ(u). Тогда получим 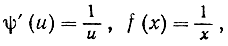 так что
так что
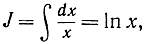
или
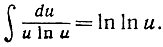
Результат можно проверить посредством дифференцирования; мы получаем:
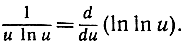
b)
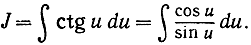
Полагая x = sin u = ψ(n), мы имеем
ψ' (u) = cos u, f(x) = x,
откуда следует
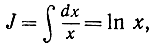
или
∫ ctg u du = ln sin u.
И этот результат проверяется дифференцированием.
c) Допустим, что задан интеграл более общего вида
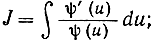
положив х = ψ(u), f(x) = x, мы найдем:
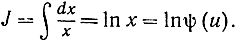
d) J = ∫ sin x cos x dx. Полагаем 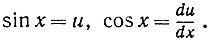
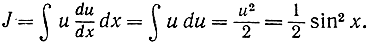
e) 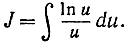 Полагаем
Полагаем 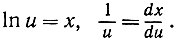 Тогда
Тогда
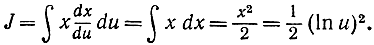
В следующих примерах мы используем формулу (I), читая ее слева направо.
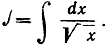
Полагаем √х = u. Тогда х = u2 и 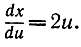 Поэтому
Поэтому
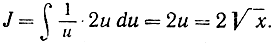
g) С помощью подстановки х = аu, где а - постоянная, получаем:
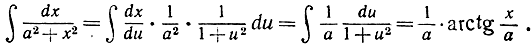
h) 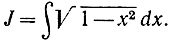 Полагаем
Полагаем 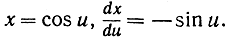
В таком случае
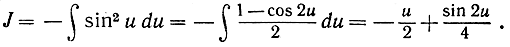
Принимая во внимание, что
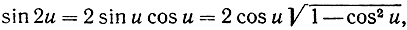
приходим к формуле
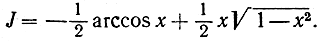
Вычислите следующие интегралы и проверьте результаты посредством дифференцирования:
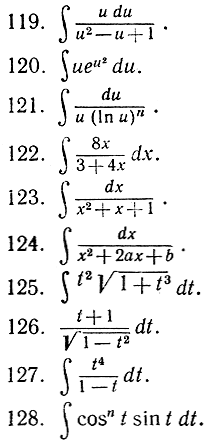
129. Докажите, что
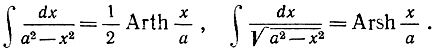
(Сравните с примерами g), h).)
В) Правило дифференцирования произведения (стр. 462)
(p(x)q(x))' = p(x)*q'(x) + p'(x)*q(x)
в интегральной форме записывается следующим образом:
p(x)*q(x) = ∫p(x)*q'(x) + ∫ p'(x)*q(x) dx,
или же
∫p(x)*q'(x) dx = p(x)*q(x) - ∫ p'(x)*q(x) dx.(II)
В этой форме оно называется правилом интегрирования по частям. Это правило бывает полезно в тех случаях, когда функция, стоящая под интегралом, имеет вид p(x)q'(x), причем неопределенный интеграл q(x) от функции q'(x) известен. Формула (II) сводит проблему неопределенного интегрирования функции р(х) q' (x) к проблеме интегрирования функции р'(х) q(x), что часто оказывается более простым.
a) J = ∫ ln x dx. Положим р(х) = ln х, q'(x) = 1, так что q(x) = x. Тогда формула (II) нам дает
∫ ln х dx = х ln х - ∫ x/x dx = х ln x - x.
b) J = ∫ x ln x dx. Положим р(х) = ln х, q'(x) = x. Тогда
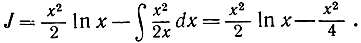
c) J = ∫ x sin x dx. На этот раз положим p(x) = x, q(x) = -cos x и получим
∫ x sin x dx = -x cos x + sin x.
Вычислите по частям следующие интегралы:
130. ∫ xex dx.
131. ∫ x2 cos x dx.
(Указание. Примените (II) дважды.)
132. ∫ ха log x dx (a≠ -1).
133. ∫ x2 ex dx.
(Указание. Воспользуйтесь упражнением 130.)
Интегрируя по частям ∫ sin mx dx, мы получаем замечательную формулу для числа π в виде бесконечного произведения. Напишем функцию sin x в виде sin m-1 x*sin х и проинтегрируем по частям в пределах от 0 до π/2.
Тогда получим:
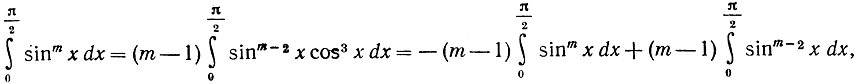
или же
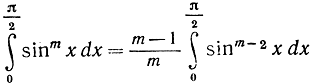
(так как первый член в правой части (II), pq, обращается в нуль при х = 0 и 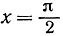 Применяя повторно последнюю формулу, найдем следующие значения интегралов
Применяя повторно последнюю формулу, найдем следующие значения интегралов 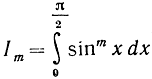 (формулы различаются в зависимости от четности n):
(формулы различаются в зависимости от четности n):
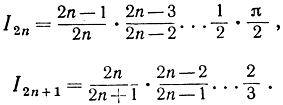
Так как 0<sin x<1 при 0<x<π/2, то sin2n-1x>sin2n x>sin2n+1x и, следовательно,
I2n-1>I2n>I2n+1,(см. стр. 448)
или
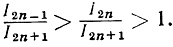
Подставляя в эти неравенства вычисленные значения интегралов, получаем
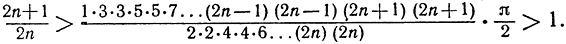
Остается положить n→∞; тогда, убедившись, что средняя часть неравенства стремится к 1, мы получаем следующее, принадлежащее Уоллису, представление для числа π/2:
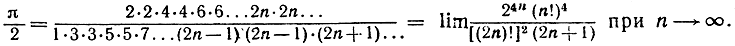
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'