Максимумы и минимумы

84. Найдите кратчайший путь от точки Р к точке Q на рис. 178, если требуется подойти по очереди n раз к каждой из двух данных прямых (см. стр. 364).

85. Найдите кратчайший путь от точки Р к точке Q внутри остроугольного треугольника, если требуется подойти к каждой стороне в данном порядке (см. стр. 364).

86. Наметьте линии уровня и удостоверьтесь в существовании по меньшей мере двух седловых точек на поверхности, расположенной над трех-связной областью, границы которой находятся на одном и том же уровне (см. стр. 378). И здесь нужно сделать исключение для того случая, когда касательная плоскость к поверхности горизонтальна вдоль некоторой кривой.

87. Исходя из двух произвольных положительных рациональных чисел а₀, b₀, одну за другой построить пары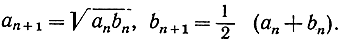

Доказать, что они образуют последовательность вложенных интервалов. (Предел этой последовательности при n→∞ есть так называемое арифметико-геометрическое среднее чисел а₀, b₀, игравшее большую роль в ранних исследованиях Гаусса.)

88. Найти длину всего графика на рис. 219 и сравнить с суммой длин двух диагоналей квадрата.

^* 89. Исследовать, при каких условиях, наложенных на точки A₁, A₂, A₃, A₄, получается схема рис. 216 и при каких - схема рис. 218.

^* 90. Найти такие расположения пяти точек, для которых существовали бы различные минимальные системы путей, удовлетворяющие угловым условиям. Некоторые из этих систем будут соответствовать относительным минимумам (см. стр. 375).

91. Докажите неравенство Шварца

(а₁b₁ + ... + a_nb_n)² ≤ (a₁² + ... + a²_n)(b₁² + ... + b²_n),

справедливое для каких угодно а_i и b_i; докажите, что знак равенства возможен только при условии пропорциональности между числами а_i и b_i. (Указание. Обобщите алгебраическую формулу, приведенную в упражнении 8.)

^* 92. Исходя из n положительных чисел х₁, ..., х_n, строим выражения s_k, определяемые формулами

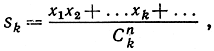
причем в числителе стоит сумма всевозможных произведений, составленных из всех сочетаний n чисел по k. Докажите, что

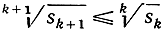
и что знак равенства возможен только в случае равенства всех чисел x_i.

93. При n = 3 эти неравенства сводятся к следующим:

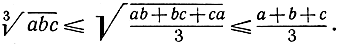
Какие отсюда вытекают экстремальные свойства куба?

^* 94. Найти дугу кривой минимальной длины, соединяющую две точки А, В и вместе с прямолинейным отрезком АВ ограничивающую наперед заданную площадь. (Ответ: Дуга должна быть круговая.)

^* 95. Даны два отрезка АВ и А'В'. Найти дуги кривых, соединяющие А с В и А' с В', ограничивающие вместе с отрезками данную площадь и обладающие наименьшей суммой длин. (Ответ: Дуги должны быть круговыми, с одинаковыми радиусами.)

^* 96. Тот же вопрос - при каком угодно числе отрезков АВ, А'В' и т. д.

^* 97. Даны две прямые, пересекающиеся в точке О. Найти на каждой из них по точке А и В и затем соединить эти точки кривой линией таким образом, чтобы при заданной площади, ограниченной кривой и обеими прямыми, длина дуги была минимальной. (Ответ: Дуга должна быть круговой и перпендикулярной к обеим прямым.)

^* 98. Тот же вопрос со следующим видоизменением: обратить в минимум требуется не длину кривой АВ, а весь периметр фигуры, т. е. сумму дуги АВ и отрезков ОА и ОВ. (Ответ: Дуга - по-прежнему круговая, но выпячивается наружу, касаясь отрезков в их концах.)

^* 99. Обобщите эту проблему на случай нескольких угловых секторов.

^* 100. Установите, что "почти плоские" поверхности на рис. 240 не являются в точности плоскими, кроме стабилизирующей поверхности в центре куба. (Замечание. Определить эти поверхности аналитически представляет заманчивую, еще не решенную проблему. То же относится и к поверхностям на рис. 251. Что касается рис. 258, то здесь в самом деле имеется 12 симметрических плоскостей, образующих по диагоналям углы в 120°.)

Некоторые дополнительные предложения по поводу опытов с мыльными пленками. Сделайте опыты, указанные на рис. 256 и 257, при числе стержней, большем трех. Изучите, что происходит в предельных случаях, когда объем воздуха становится все меньше. Экспериментируйте с непараллельными плоскостями и другими поверхностями. Раздувайте центральный кубик на рис. 258, пока он не наполнит весь большой куб и не выпятится за пределы граней; потом выдувайте из него воздух, пытаясь обратить процесс.

^* 101. Найти два равнобедренных треугольника с данной суммой периметров и с минимальной суммой площадей. (Ответ: Треугольники должны быть конгруэнтны. Воспользуйтесь методами дифференциального исчисления.)

^* 102. Найти два треугольника с данной суммой периметров и максимальной суммой площадей. (Ответ: Один треугольник вырождается в точку, другой должен быть равносторонним.)

^* 103. Найти два треугольника с данной суммой площадей и минимальной суммой периметров.

^* 104. Найти два равносторонних треугольника с данной суммой площадей и максимальной суммой периметров.