
Функции, пределы, непрерывность
77. Разложить в непрерывную дробь отношение ОВ:AB со стр. 152.
78. Докажите, что последовательность 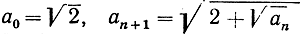 монотонно возрастает, ограничена числом B = 2 и, значит, имеет предел. Докажите, что этот предел не может быть отличен от 2 (см. стр. 328 и 359).
монотонно возрастает, ограничена числом B = 2 и, значит, имеет предел. Докажите, что этот предел не может быть отличен от 2 (см. стр. 328 и 359).
* 79. Попробуйте доказать посредством рассуждений, подобных тем, какие были приведены на стр. 350 и далее, что, какова бы ни была гладкая замкнутая кривая, всегда можно начертить квадрат, стороны которого будут касаться кривой.
80. Функция u = f(x) называется вогнутой, если середина отрезка, соединяющего две любые точки соответствующего графика, лежит выше самого графика. Например, функция u = ех - вогнутая (рис. 278), тогда как функция u = ln х (рис. 277) - не вогнутая.
Докажите, что функция u = f(x) вогнута в том и только в том случае, если
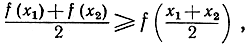
причем равенство имеет место только при x1 = x2.
* 81. Докажите, что в случае вогнутой функции оправдывается и более общее неравенство
где λ1, λ2 - две постоянные, подчиненные ограничениям λ1 + λ2 = 1, λ1≥, λ2≥0. Это равносильно утверждению, что ни одна из точек отрезка,, соединяющего две произвольные точки графика, не лежит ниже кривой.
82. Пользуясь условием упражнения 80, доказать, что функции 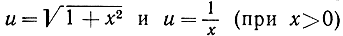 вогнуты, т. е. что при положительных значениях х1 и х2
вогнуты, т. е. что при положительных значениях х1 и х2
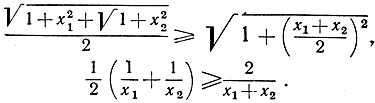
83. Докажите то же для u = х2, u = хn при х >0; для u = sin x при π≤x≤2π; для u = tg x при 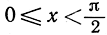 и для
и для 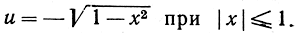
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'