Проективная и неевклидова геометрия

43. Найти все значения двойного отношения λ четырех гармонических точек, если эти точки подвергаются всевозможным перестановкам.

(Ответ:)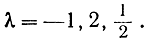

44. При каких расположениях четырех точек какие-нибудь два из шести значений двойного отношения на стр. 207 совпадают между собой? (Ответ: Только при λ = -1 или λ = 1; имеется только одно мнимое значение λ, при котором 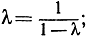ему соответствует "эквигармоническое" двойное отношение.)

45. Удостоверьтесь, что равенство двойного отношения (ABCD) единице означает совпадение точек С и D.

46. Докажите утверждения, касающиеся двойного отношения плоскостей, приведенные на стр. 208.

47. Докажите: если точки Р и Р' взаимно обратны относительно окружности и диаметр А В коллинеарен с точками Р и Р', то четверка точек А, В, Р, Р' гармоническая. (Указание. Воспользуйтесь формулой (2) на стр. 249; предположите, что данная окружность единичная и что АВ - ось координат.)

48. Найдите координату четвертой гармонической точки относительно данных точек P₁, P₂, Р₃. Что случится, если Р₃ станет приближаться к середине отрезка P₁P₂? (См. стр. 216.)

^* 49. Попробуйте развить теорию конических сечений, исходя из сфер Данделена. В частности, докажите, что все они, за исключением окружностей, являются геометрическим местом точек, для которых расстояния от данной точки и от данной прямой находятся в постоянном отношении k. При k>1 получается гипербола, при k = 1 - парабола, при k<1 - эллипс. Прямая l получается как пересечение плоскости конического сечения с плоскостью того круга, по которому сфера Данделена соприкасается с конусом. (Именно по той причине, что круг приходится особо оговаривать как предельный случай, не совсем удобно принимать указанное свойство в качестве определения конических сечений, что, впрочем, делается довольно часто.)

50. Обсудите следующее положение: "коническое сечение, рассматриваемое одновременно как множество точек и как множество касательных прямых, само себе двойственно" (см. стр. 238).

^* 51. Попробуйте доказать теорему Дезарга, выполняя предельный переход от пространственной конфигурации, изображенной на рис. 73 (см. стр. 202).

^* 52. Сколько можно провести в пространстве прямых, пересекающихся с данными четырьмя прямыми? Как их можно характеризовать? (Указание. Через три данные прямые проведите гиперболоид; см. стр. 245).

^* 53. Возьмем в качестве круга Пуанкаре единичный круг в комплексной плоскости. Пусть z₁ и z₂ - какие-то две точки внутри этого круга, а ω₁ и ω₂ - точки пересечения с окружностью "прямой линии", проходящей

через z₁ и z₂. Тогда двойное отношение 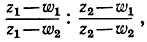в соответствии с упражнением 8 на стр. 125, имеет действительное значение; докажите это. По определению его логарифм есть гиперболическое расстояние между гх и г2.

^* 54. С помощью инверсии преобразуйте круг Пуанкаре в верхнюю полуплоскость. Исследуйте эту полуплоскость как модель Пуанкаре и непосредственно, исходя из преобразования инверсии.