Геометрические построения

35. Докажите невозможность построения с помощью только циркуля и линейки чисел 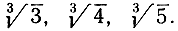Доказать, что построение числа √а возможно только в том случае, если а есть куб рационального числа (см. стр. 197 и далее).

36. Найти стороны правильных 3*2ⁿ-угольников и 5*2ⁿ-угольников. Дать характеристику последовательно вводимых полей расширения.

37. Доказать невозможность трисекции с помощью только циркуля и линейки углов в 120° или 30°. (Указание для случая угла в 30°: мы приходим к уравнению 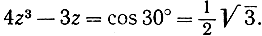Введя новую переменную u = z√3 , вы получите уравнение, с которым рассуждайте так же, как на стр. 167).

38. Доказать невозможность построения правильного 9-угольника.

39. Установить, что инверсия точки Р(х, y) в точку Р'(х', y') относительно окружности с центром в начале координат и радиусом r дается формулами:

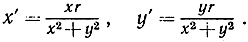
Решите эти уравнения относительно х и y.

*40. Основываясь на упражнении 39, установить аналитически, что при инверсии окружности и прямые переходят в окружности и прямые.

Проверьте, в частности, свойства а) - d) со стр. 172, а также преобразования, указанные на рис. 61.

41. Что станет с двумя семействами прямых х = const и y = const, параллельных координатным осям, при инверсии относительно единичной окружности с центром в начале? Дайте ответ без помощи аналитической геометрии и с помощью аналитической геометрии.

42. Выполните построение Аполлония в простых случаях по вашему собственному выбору. Попробуйте найти решение в аналитической форме, как было указано на стр. 154.