Аналитическая геометрия

Внимательное выполнение следующих упражнений, сопровождаемое чертежами и числовыми примерами, даст возможность овладеть элементами аналитической геометрии. Определения и простейшие факты из тригонометрии предполагаются известными.

Во многих случаях целесообразно представлять себе прямые или отрезки направленными от одной точки к другой. Под направленной прямой PQ (или направленным отрезком РQ) мы будем понимать прямую (или отрезок), направленную от Р к Q. Если разъяснения отсутствуют, то предполагается, что направленная прямая l имеет безразлично какое, но вполне определенное направление; только в случае направленной оси x неизменно принимается, что она направлена от начала 0 к любой ее точке с положительной координатой х, и аналогично для оси y. О направленных прямых (или отрезках) мы будем говорить, что они параллельны в том и только в том случае, если они направлены одинаково. Направление направленного отрезка на направленной прямой может быть фиксировано знаком + или -, присоединяемым к расстоянию между конечными точками отрезка, смотря по тому, совпадает или не совпадает направление отрезка с направлением прямой. Целесообразно понятие "отрезок PQ" обобщить и на тот случай, когда точки Р и Q совпадают; таким "отрезкам" приписывается длина нуль и не приписывается никакого направления.

16. Докажите: если Р₁ (х₁, y₁) и Р₂ (х₂, y₂) - какие-нибудь две точки, то координаты середины отрезка Р₁Р₂-P₀(x₀, y₀) определяются формулами 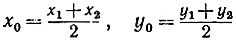Установите более общее положение: если точки Р₁ и Р₂ различны, то та точка Р₀ на направленной прямой Р₁Р₂, для которой отношение направленных отрезков 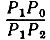равно k, имеет координаты

(Указание. Примите во внимание свойство пропорциональности отрезков при пересечении сторон угла параллельными прямыми.)

Таким образом, все точки на прямой Р₁Р₂ имеют координаты вида x = λ₁x₁ + λ₂x₂, y = λ₁y₁ + λ₂y₂, причем λ₁ + λ₂ = 1. При λ₁ = 1 и λ₂ = 0 получаются соответственно точки Р₁ и Р₂. Отрицательным значениям λ₁ соответствуют точки по ту сторону Р₂, отрицательным значениям λ₂ - точки по ту сторону Р₁, т. е. точки, лежащие на прямой Р₁Р₂ вне отрезка

17. Охарактеризовать подобным же образом положение точки на прямой в зависимости от числовых значений k.

В такой же мере существенно использовать положительные и отрицательные числа для обозначения направленных вращений. По определению в качестве положительного направления вращения избирается то, которое направленную ось х переводит в ось y после поворота на 90°. При обыкновенном расположении осей (когда ось х направлена вправо, а ось у - вверх) положительное вращение направлено против часовой стрелки. Мы определим теперь угол от направленной прямой l₁ к направленной прямой l₂ как угол, на который нужно повернуть прямую l₁, чтобы она стала параллельной прямой l₂. Разумеется, этот угол определен лишь с точностью до величин, кратных 360°. Так, угол между осью х и осью y равен 90° или -270° и т. д. Вместо "угол от l₁ до l₂" мы будем говорить короче: "угол между l₁ и l₂", учитывая, конечно, что "угол между l₁ и l₂" и "угол между l₂ и l₁" различаются знаком.

18. Пусть α обозначает угол между направленной осью х и направленной прямой l. Пусть Р₁, Р₂ - две точки на l и d - направленное расстояние от Р₁ до Р₂. Покажите, что

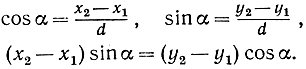
Если прямая l не перпендикулярна к оси х, то наклон l определяется формулой

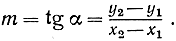
Значение m не зависит от того, как направлена прямая l, так как tg α = tg (α+180°), или, что равносильно,

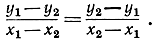
19. Докажите: наклон прямой равен нулю, положителен или отрицателен, смотря по тому, пойдет ли прямая, параллельная данной и проходящая через начало, по оси x или через первый и третий квадранты, или через второй и четвертый квадранты.

Мы условимся различать две "стороны" направленной прямой - положительную и отрицательную (менее удобно было бы говорить о положительной и отрицательной полуплоскостях). Пусть Р - какая-нибудь точка, не лежащая на прямой l, и Q - основание перпендикуляра к l, проведенного через Р. Тогда Р лежит с положительной или с отрицательной стороны l, смотря по тому, будет ли угол между l и направленной прямой QP равен 90° или -90°.

Затем мы определим уравнение направленной прямой l. Через начало О проведем прямую m, перпендикулярную к l, и направим ее так, чтобы угол между m и l был равен 90°. Обозначим через Р угол между направленной осью х и прямой m. Тогда α = 90° + β, sin α = cos β, cos α = -sin β. Пусть R (x₁, y₁) есть точка пересечения l и m. Обозначим через d направленное расстояние OR на направленной прямой m.

20. Показать, что d положительно в том и только в том случае, если начало О находится с отрицательной стороны l.

Мы имеем: x₁ = d cos β, y₁ = d sin β (см. упражнение 18). Отсюда следует (х-х₁) sin α = (y-y₁) cos α, или

что приводит окончательно к уравнению

Это - нормальная форма уравнения прямой l. Следует заметить, что это уравнение не зависит от направления прямой l, так как изменение ее направления повлекло бы за собой изменение знаков у всех членов в левой части, причем уравнение осталось бы тем же самым.

Умножая нормальное уравнение на произвольный множитель, мы получаем общую форму уравнения прямой линии

Чтобы получить, обратно, из этой общей формы геометрически содержательную нормальную форму, придется умножить обе части уравнения на такой множитель, чтобы коэффициенты при х и y свелись к величинам вида cos β и sin β, квадраты которых в сумме составляют 1. Таким множителем является 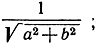он придает уравнению нормальную форму

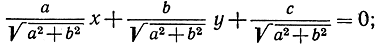
здесь мы имеем:

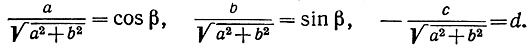
21. Доказать, что: а) кроме 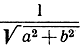и 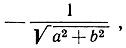не существует иных множителей, приводящих общее уравнение к нормальной форме; b) выбор того или иного множителя фиксирует направление прямой; с) после того как выбор того или иного множителя сделан, можно сказать, что начало О находится с положительной или с отрицательной стороны прямой или находится на самой прямой, смотря по тому, будет ли d отрицательным, положительным или нулем.

22. Доказать непосредственно, что прямая с наклоном т, проходящая через данную точку Р₀ (х₀, y₀), представляется уравнением

Доказать, что прямая, проходящая через две данные точки Р₁(х₁, y₁) и Р₂ (х₂, y₂), имеет уравнение

Условимся: координата х точки пересечения прямой с осью х называется "отрезком на оси х"; аналогично относительно "отрезка на оси y".

23. Докажите, что, деля общее уравнение, полученное в упражнении 20, на надлежащим образом подобранное число, получим уравнение прямой "в отрезках на осях"

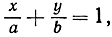
причем а и b - отрезки, которые прямая образует соответственно на оси х и оси y. Могут ли быть исключительные случаи?

24. Покажите, что в результате подобной же процедуры уравнение всякой прямой, не параллельной оси y, может быть "решено относительно y":

(Если же прямая параллельна оси y, то ее уравнению можно придать вид х = а.)

25. Предположим, что ах + by + с = 0 и а'х + b'у + с' = 0 - уравнения двух данных прямых l и l'; пусть m и m' - соответственно их наклоны. Докажите, что l и l' параллельны или перпендикулярны, смотря по тому, будет ли: а) m = m' или mm' = -1, b) ab' - a'b = 0 или aa' + bb' = 0. (Обратите внимание, что формулировка b) пригодна и для того случая, когда у прямой "нет никакого наклона", т. е. она параллельна оси y.

26. Установите, что уравнение прямой, проходящей через точку P₀(x₀, y₀) и параллельной данной прямой l с уравнением ах + by + с = 0 имеет вид ах + by = ax₀ + by₀. Установите, что если условие параллельности заменить условием перпендикулярности, то соответствующее уравнение примет вид bх - аy = bх₀ - аy₀. (Интересно заметить, что если уравнение l написано в нормальной форме, то в такой же форме получается и новое уравнение.)

27. Пусть уравнения x cos β + y sin β - d = 0 и ах + by + с = 0 представляют в нормальной форме и в общей форме одну и ту же прямую l. Докажите, что направленное расстояние h от l до некоторой точки Q(u, v) дается формулой

или же

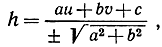
и что h - положительное или отрицательное число, смотря потому, лежит ли Q с положительной или с отрицательной стороны, направленной прямой l (причем направление l фиксируется или углом р, или выбором знака при 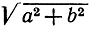). (Указание. Напишите в нормальной форме уравнение прямой m, проходящей через Q и параллельной m, и затем определите расстояние между l и m.)

28. Предположим, что l (х, y) = 0 есть сокращенная запись уравнения ах + by + с = 0 некоторой прямой l; аналогично - для l' (х, y) = 0. Пусть λ и λ' - постоянные числа, причем λ + λ' = 1. Докажите, что если прямые l и l' пересекаются в точке Р₀ (х₀, y₀), то всякая прямая, проходящая через Р₀, имеет уравнение вида

и, обратно, что всякая такая прямая однозначно определяется выбором пары значений λ и λ'. (Указание. В том и только в том случае Р₀ лежит на l, если l(х₀, y₀) = ах₀ + by₀ + с = 0.) Что представляет уравнение в случае, если l и l' параллельны? (Заметьте, что в условии λ + λ' = 1 нет никакой необходимости: оно служит только для того, чтобы каждой прямой, проходящей через Р₀, соответствовало одно определенное уравнение.)

29. Воспользуйтесь результатами предыдущего упражнения для того, чтобы написать уравнение прямой, проходящей через точку пересечения Р₀ прямых l и l' и еще через другую точку Р₁ (х₁, y₁), не находя при этом координат Р₀. (Указание. Определите λ и λ' из условий λl (х₁, y₁) + λ'l'(х₁, y₁) = 0, λ + λ' = 1. Сделайте проверку, определяя координаты Р₀ (см. стр. 104) и устанавливая затем, что Р0 лежит на прямой, уравнение которой вы нашли.)

30. Докажите, что уравнения биссектрис углов, образованных пересекающимися прямыми l и l', имеют вид

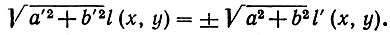
(Указание. См. упражнение 27.), Что представляют эти уравнения, если прямые l и l' параллельны?

31. Двумя способами выведите уравнение прямой, проходящей через середину отрезка Р₁Р₂ и к нему перпендикулярной: а) Напишите уравнение Р₁Р₂; найдите координаты середины Р₀ отрезка Р₁Р₂; напишите уравнение прямой, проходящей через Р₀ и перпендикулярной к Р₁Р₂. b) Выразите в виде уравнения то условие, что расстояние (стр. 100) между Р₁ и какой-нибудь точкой Р (х, y) искомой прямой равно расстоянию между Р₂ и Р; возведите обе части равенства в квадрат и сделайте упрощения.

32. Двумя способами выведите уравнение окружности, проходящей через три точки Р₁, Р₂, Р₃, не лежащие на одной прямой: а) Напишите уравнение перпендикуляров, проведенных к отрезкам Р₁Р₂ и Р₂Р₃ через их середины; найдите координаты центра как точки пересечения этих перпендикуляров, определите радиус как расстояние между центром и Р₁. b) Искомое уравнение должно иметь вид х² + y² - 2ах - 2by = k (см. стр. 120). Так как каждая из данных точек лежит на окружности, то мы должны иметь

так как точки лежат на кривой в том и только в том случае, если ее координаты удовлетворяют уравнению кривой. Затем решите систему относительно а, b, k.

33. Напишем уравнение эллипса с большей осью 2р, малой осью 2q и фокусами F (-е, 0) и F' (е, 0), причем е² = р² - q². Воспользуемся расстояниями r и r' произвольной точки Р (х, y) кривой от F и F'. По определению эллипса r + r' = 2p. С помощью формулы для расстояния между точками (стр. 119) установите, что

Так как

то отсюда выведите соотношение 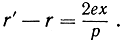Решая последнее уравнение совместно с уравнением r + r' = 2р, вы получите важные формулы

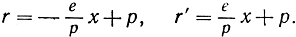
Так как (опять по формуле расстояния) r² = (х - е)² + y², то можно будет приравнять полученное выражение для r² выражению 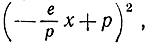полученному раньше, и тогда будем иметь:

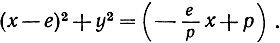
Раскройте скобки, соберите члены, подставьте р² - q² вместо е² и сделайте упрощения. Приведите окончательно уравнение к виду

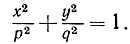
Сделайте аналогичные вычисления для гиперболы, определяя ее как геометрическое место точек Р, для которых абсолютное значение разности r - r' равно данному числу 2р. Но в этом случае е² = р² + q².

34. Парабола определяется как геометрическое место точек, расстояние которых отданной прямой (директрисы) равно расстоянию отданной точки (фокуса). Выбрав в качестве директрисы прямую х = -а, а в качестве фокуса точку F (а, 0), покажите, что уравнение параболы может быть написано в виде