Арифметика и алгебра

1. Откуда мы знаем, что, как говорится на стр. 87, никакая степень 10 не делится на 3?

2. Докажите, что принцип наименьшего целого числа вытекает как следствие из принципа математической индукции.

3. Применяя биномиальную теорему к разложению (1 + 1)ⁿ, докажите, что С₀ⁿ + С₁ⁿ + С₂ⁿ + ... + С_nⁿ = 2ⁿ.

4. ^* Задумайте какое-нибудь число z = abc ... , составьте сумму его цифр а + b + с ..., вычтите ее из z,, вычеркните одну цифру из остатка и обозначьте через ω сумму оставшихся цифр. Нельзя ли найти правило для того, чтобы определить вычеркнутую цифру, зная только значение ω? (Будет не вполне определенный случай, если ω = 0.) Как и многое другое из того, что связано со сравнениями, этот пример пригоден в качестве "развлекательной задачи с угадыванием".

5. Арифметической прогрессией первого порядка называется такая последовательность чисел а, а + d, а + 2d, а + 3d, ... , что разность между следующим членом и предыдущим постоянна. Арифметическая прогрессия второго порядка есть такая числовая последовательность а₁, а₂, а₃, ..., что разности a_i+1 - a_i образуют арифметическую прогрессию первого порядка. Вообще, арифметической прогрессией порядка k называют последовательность, обладающую тем свойством, что разности рядом стоящих членов образуют арифметическую прогрессию (k-1)-го порядка. Проверить, что квадраты натуральных чисел образуют арифметическую прогрессию 2-го порядка, и затем установить, по математической индукции, что k-e степени натуральных чисел образуют арифметическую прогрессию порядка k. Доказать, что всякая последовательность чисел а_n, где а_n = с₀ + с₁n + с₂n² + ... + c_kn^k и все с - постоянные, есть арифметическая прогрессия порядка k. ^*Доказать обратное утверждение для случая k = 2, k = 3, для любого k.

6. Доказать, что суммы n первых членов арифметической прогрессии порядка к образуют арифметическую прогрессию (k+1)-го порядка.

7. Сколько делителей у числа 10 296?

8. Пользуясь алгебраической формулой

докажите с помощью индукции, что любое целое число r = а₁а₂ ... а_n может быть представлено как сумма двух квадратов, если каждый из множителей а обладает тем же свойством. Проверьте это на примерах

принимая во внимание, что

Если возможно, найдите два различных представления этих чисел как суммы двух квадратов.

9. Воспользуйтесь результатом предыдущего упражнения для того, чтобы по заданным пифагоровым тройкам чисел строить новые.

10. Составьте правила делимости для систем счисления с основаниями 7, 11, 12.

11. Докажите: неравенство r>s между двумя положительными рациональными числам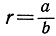и и 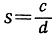равносильно неравенству ас-bd>0.

12. Докажите: если r и s - положительные числа, причем r<s, то

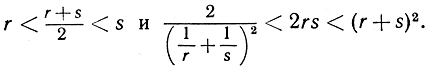
13. Предполагая, что r - какое угодно комплексное число, докажите с помощью индукции, что 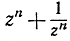может быть представлено как полином степени n относительно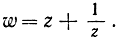

14. ^*Если положим ради краткости E(φ) = cos φ + i sin φ, то получим [Е(φ)]^m = Е(mφ). Воспользовавшись этой формулой, а также формулой для суммы геометрической прогрессии (стр. 37; эта формула сохраняется и для комплексных величин), докажите, что

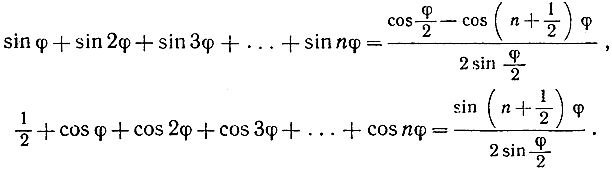
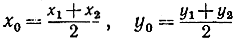
15. Что получится из формулы упражнения 3 на стр. 42, если подставить q = Е(φ)?