3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin х в виде бесконечного произведения

Ряды, члены которых являются простыми комбинациями целых чисел, особенно интересны. В качестве примера рассмотрим "гармонический ряд"

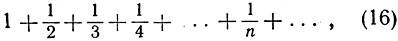
отличающийся от известного нам ряда, сумма которого равна ln 2, только знаками членов, стоящих на четных местах.

Поставить вопрос, сходится ли этот ряд, все равно, что спросить себя, стремится ли к конечному пределу последовательность чисел

где

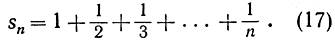
Несмотря на то что по мере продвижения по ряду (16) члены его приближаются к 0, легко увидеть, что ряд этот не сходится. Действительно, взяв достаточное количество членов, мы можем превысить любое положительное число; таким образом, s_n возрастает беспредельно, и, значит, ряд (16) "расходится к бесконечности". Чтобы в этом убедиться,заметим, что

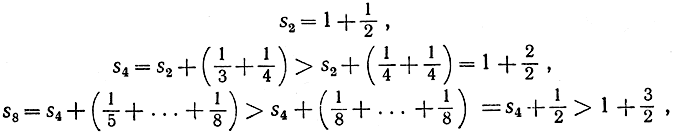
и, вообще,

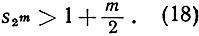
Таким образом, например, частные суммы s_2^m превышают 100, если только m≥200.

Если гармонический ряд расходится, то, с другой стороны, можно доказать, что ряд

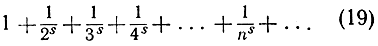
сходится при всяком значении s, большем, чем 1, и сумма его, рассматриваемая как функция переменного s, есть так называемая дзета-функция

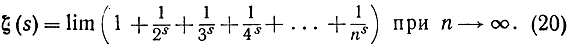
Эта функция, очевидно, определена только при s>1.

Существует важное соотношение между дзета-функцией и простыми числами, которое мы выведем, исходя из свойств геометрической прогрессии. Пусть р есть какое-нибудь простое число; тогда при s≥1

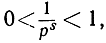
так что

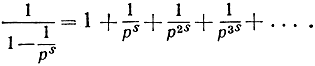
Перемножим такого рода равенства, написанные для всех простых чисел р = 2, 3, 5, 7, ... (не задаваясь вопросом о законности такой операции). В левой части мы получим "бесконечное произведение"

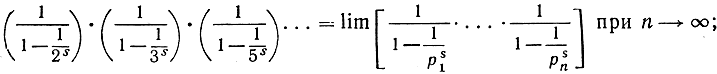
в то же время в правой части мы получаем ряд

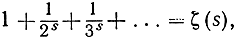
в силу того обстоятельства, что каждое целое число, большее, чем 1, может быть единственным образом представлено как произведение степеней различных простых чисел. Итак, нам удалось выразить дзета-функцию в виде произведения

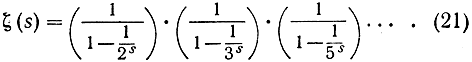
Если бы существовало только конечное число простых чисел, скажем, p₁, p₂, p₃, ..., p_r, то произведение в правой части формулы (21) было бы обыкновенным конечным произведением и имело бы поэтому конечное значение даже при s = 1. Однако мы видели, что дзета-ряд при s = 1

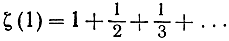
расходится, стремясь к бесконечности. Это рассуждение, которое легко превратить в строгое доказательство, показывает, что существует бесконечное множество простых чисел. Конечно, это доказательство гораздо запутаннее и искусственнее, чем данное Евклидом (см. стр. 46). Но оно столь же привлекательно, как трудный подъем на вершину горы, которая могла бы быть достигнута с другой стороны по комфортабельной дороге.

С помощью бесконечных произведений, подобных тому, которое дается формулой (21), функции иногда выражаются так же удобно, как и с помощью бесконечных рядов.

Другое бесконечное произведение, открытие которого представляет собой еще одно из достижений Эйлера, относится к тригонометрической функции sin х. Чтобы понять найденную Эйлером формулу, мы начнем со следующего замечания относительно многочленов. Если

есть многочлен степени n, имеющий n различных нулей х₁, ..., х_n, то, как известно из алгебры, функция f (x) может быть разложена на линейные множители

(см. стр. 129). Вынося за скобку произведение x₁x₂...x_n, мы можем написать

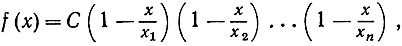
где С - постоянная, равная а₀, что легко установить, положив х = 0. Далее возникает вопрос: возможно ли аналогичное разложение уже не для полиномов, а для более сложных функций f(x)? (В общем случае ответ не может быть утвердительным, в чем легко убедиться на примере показательной функции, которая вовсе не имеет нулей, поскольку е^x≠0 при любых значениях х.) Эйлер открыл, что для функции синус такое разложение возможно. Чтобы написать формулу в ее простейшем виде, мы рассмотрим не sin x, a sin πx. Последняя функция имеет нулями точки π = 0, ±1, ±2, ±3, ..., так как sin πn = 0 при всех целых n; иных же нулей она не имеет никаких. Формула Эйлера устанавливает соотношение

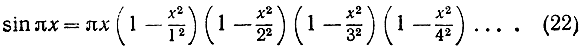
Стоящее справа бесконечное произведение сходится при всех значениях х и является одной из красивейших формул математики. При 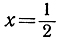формула дает

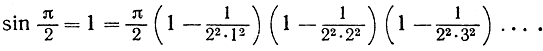
Если мы напишем

то после небольших преобразований получим произведение Уоллиса

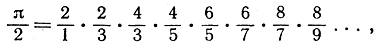
упомянутое на стр. 333.

За доказательствами всех этих соотношений мы вынуждены направить читателя к руководствам по анализу (см. также стр. 549-550).