§ 4. Доказательство теоремы о простых числах на основе статистического метода

Применяя математические методы к изучению явлений природы, обычно удовлетворяются такими рассуждениями, в ходе которых цепь строгих логических доводов прерывается более или менее правдоподобными допущениями. И даже в чистой математике можно подчас встретить рассуждение, которое хотя и не обеспечивает строгого доказательства, но все же, несмотря на это, подсказывает правильное решение и дает направление, в котором можно искать это строгое доказательство.

Именно таков характер решения задачи о брахистохроне, данного Якобом Бернулли (см. стр. 416), а также очень многих других проблем раннего периода развития анализа.

Пользуясь процедурой, типичной для прикладной математики и в особенности для статистической механики, мы приведем сейчас одно рассуждение, которое сделает по меньшей мере правдоподобной справедливость знаменитого гауссова закона о распределении простых чисел. (Упомянутая процедура была подсказана одному из авторов специалистом по экспериментальной физике Густавом Герцем.) Эта теорема, рассмотренная с эмпирической точки зрения в дополнениях к главе I, утверждает, что число А(n) простых чисел, не превышающих n, асимптотически равно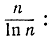

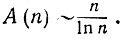
Под этим подразумевается то, что отношение 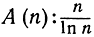стремится к пределу при стремлении n к бесконечности.

Допустим прежде всего, что существует математический закон распределения простых чисел, обладающий следующим свойством: при больших значениях n определенная выше функция А(n) приблизительно равна интегралу 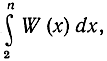где W(x) можно назвать функцией, измеряющей "плотность" простых чисел. (В качестве нижнего предела интеграла мы выбрали число 2, так как при х<2 имеем, очевидно, А(х) = 0.) Более точно o пусть х - растущая величина и Δх - другая растущая величина, но такая, что порядок возрастания х больше порядка возрастания Ах. (Например, можно принять, что Δx = √х.) Сделаем, далее, гипотезу, что распределение простых чисел настолько равномерно, что число простых чисел в промежутке от x до х + Δх приближенно равно выражению вида W(x)Δx, и даже более того, что функция W(x) изменяется так плавно, что интеграл 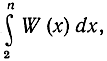может быть заменен соответствующей интегральной "ступенчатой" суммой, не изменяя своего асимптотического значения. После этих предварительных замечаний мы подготовлены для того, чтобы начать наше рассуждение.

Мы уже доказали ранее (стр. 509), что при больших целых числах выражение ln (n!) асимптотически равно произведению n ln n:

Мы дадим сейчас другую асимптотическую формулу для ln (n!), выражающуюся через простые числа, а затем сравним оба выражения. Сосчитаем, сколько раз произвольное простое число р, меньшее, чем n, входит множителем в целое число n! = 1*2*3 ... n. Обозначим символом [а]_р наибольшее целое число k, такое, челится на р^k. Из того, что разложение любого целого числа на простые числа единственно, вытекает зависимость [ab]^p = [а]_р + [b]_p при любых целых а и b. Отсюда следует

В последовательности 1, 2, 3, ..., n члены, делящиеся на р^k, имеют вид p^k, 2p^k, 3p^k, ...; их число N_k при больших n приближенно равно ⁿ/_p^k.

Из этих членов число M^k таких, которые делятся на p^k, но не делятся на более высокие степени р, равно разности N_k-N_k+1. Следовательно, имеем

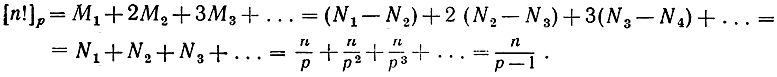
(Само собой разумеется, что эти равенства - только приближенные.) Отсюда следует, что при больших n число n! приближенно выражается произведением всех выражений вида 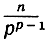с ограничением р<n. Таким образом, мы получили формулу

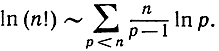
Сравнивая полученное выражение с нашей прежней асимптотической формулой для ln (n!), мы находим:

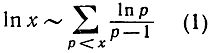
(вместо n подставлено х).

Следующим - и решающим - шагом является нахождение асимптотического выражения для правой части соотношения (1). Если х очень велико, можно промежуток от 2 до х = n разделить на большое число r достаточно больших частных промежутков точками 2 = ξ₁, ξ₂, ..., ξ_r, ξ_r+1 = x с соответственными приращениями Δξ_j = ξ_j+1-ξ_j. В каждом частном промежутке могут находиться простые числа, и каждое простое число j-го частного промежутка приближенно равно числу ξ_j. В силу нашего предположения о функции W(x), в j-м частном промежутке содержится приблизительно W(ξ_j)Δξ_j простых чисел; следовательно, сумма в правой части соотношения (1) приближенно равна выражению

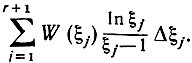
Заменив эту конечную сумму интегралом, к которому она приближается, мы получим формулу

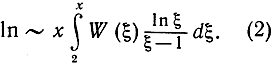
Отсюда мы теперь определим неизвестную функцию W(x). Если мы заменим значок ~ знаком обыкновенного равенства и продифференцируем обе части по х, то в силу основной теоремы анализа можно написать

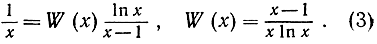
В самом начале нашего рассуждения мы предположили, что A(х) асимптотически равно интегралу

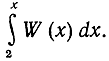
Итак, А(х) приближенно равно интегралу

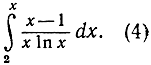
Для того чтобы вычислить этот интеграл, заметим, что функция 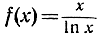имеет следующую производную:

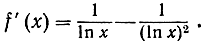
При больших значениях х два выражения

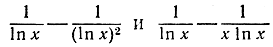
асимптотически равны, так как вторые члены в обоих выражениях много меньше первых. Следовательно, интеграл (4) будет асимптотически равен интегралу

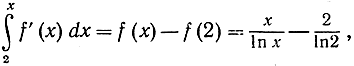
так как две сравниваемые нами функции мало отличаются на всем промежутке интегрирования. При больших значениях х членом 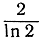как постоянным можно пренебречь, и тогда мы приходим к окончательному результату

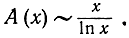
Это и есть теорема о простых числах.

Мы не можем претендовать на то, чтобы предыдущее рассуждение рассматривалось как математическое доказательство, а не как индукция. Однако более глубокий анализ приводит к следующему заключению. Нетрудно оправдать каждый, с такою смелостью сделанный нами шаг, в частности, доказать справедливость асимптотической формулы суммы и интеграла, стоящих соответственно в правых частях соотношений (1) и (2), и, наконец, обосновать шаг, ведущий от соотношения (2) к соотношению (3). Гораздо труднее доказать существование гладкой функции "плотности" W(x), которое мы постулировали в самом начале. Но раз это принято, то оценка самой функции W(x) является делом сравнительно простым; таким образом, в задаче о распределении простых чисел наиболее трудным представляется доказательство существования "плотности" W(x).