2. Формула Эйлера cos х + i sin x = e^ix

Одним из самых поразительных достижений Эйлера, полученных им на основе его формалистических манипуляций, является тесная внутренняя связь, существующая в области комплексного переменного между функциями синус и косинус, с одной стороны, и показательной функцией - с другой. Нужно заранее указать, что ни "доказательство" Эйлера, ни следующие далее доводы ни в какой мере не носят строгого характера; это - типичные для XVIII в. примеры формальных буквенных выкладок, пронизанных доверием к силе математического символизма.

Начнем с тождества Муавра, доказанного в главе II:

Подстановка 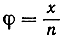приводит нас к соотношению

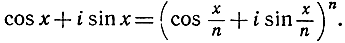
Если x зафиксировано, то cos 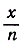будет мало отличаться от cos 0 = 1 при неограниченном возрастании n; кроме того, так как

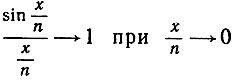
(см. стр. 340), то мы заключаем, что 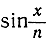асимптотически равен 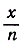. Поэтому можно считать более или менее естественным такой предельный переход

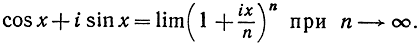
Преобразуя правую часть этого равенства согласно формуле (стр. 485)

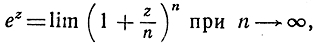
мы получим соотношение

Это и есть результат, полученный Эйлером.

Мы можем вывести эту самую формулу и другим, тоже формалистическим путем - из разложения функции e^z:

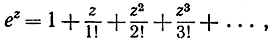
вместо z подставляя ix, где х - действительное число. Если мы вспомним, что последовательными степенями числа i являются числа i, -1, -i, + 1 и т. д., периодически, то, собирая действительные и мнимые части, мы получим:

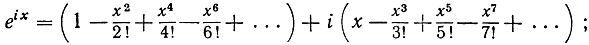
заменяя, далее, ряды в правой части их суммами cos х и sin х, мы снова получаем формулу Эйлера.

Такое рассуждение отнюдь не является настоящим доказательством соотношения (15). Против нашего второго "вывода" можно возразить, что разложение в ряд для функции e^z было проведено в предположении, что z - действительнее число; поэтому подстановка z = ix должна быть оправдана дополнительными соображениями. Точно так же полноценность первого рассуждения уничтожается тем, что формула

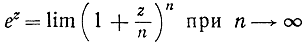
была раньше выведена только для действительных значений z.

Чтобы формула Эйлера из области чистого формализма перешла в область строгих математических истин, потребовалось развитие теории функций комплексного переменного - одного из величайших достижений XIX в. Многие другие глубокие проблемы стимулировали это далеко идущее развитие. Мы видели, например, что промежутки сходимости разложений различных функций в степенные ряды различны. Почему некоторые разложения сходятся всюду, т. е. для всех значений х, в то время как другие теряют смысл при |x|> 1?

Рассмотрим, например, геометрическую прогрессию (4), приведенную на стр. 511, которая сходится при |x|< 1. Левая часть этого равенства вполне осмысленна при х = 1, именно равна 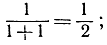в то же время ряд в правой части ведет себя очень странно: он принимает вид 1 - 1 + 1 - 1 + ... . Этот последний ряд не является сходящимся, поскольку его частные суммы колеблются между 1 и 0. Это свидетельствует о том, что функция может порождать расходящийся ряд даже в том случае, если сама она не обнаруживает какой-либо иррегулярности. Правда, функция ¹/_1+x становится бесконечной при х = - 1. И так как легко доказать, что сходимость степенного ряда в точке х = a>0 влечет за собой сходимость в промежутке -a<x<a, то мы могли бы, пожалуй, усмотреть "объяснение" странного поведения нашего разложения в разрывности функции ¹/_1+x при х = -1. Однако рассмотрим теперь функцию 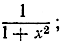она может быть разложена в ряд

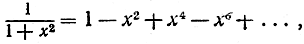
как мы убеждаемся, подставляя х² вместо х в формулу (4). Полученный ряд тоже сходится при |x|< 1; вместе с тем при х = 1 он снова приводит к ряду 1 - 1 + 1 - 1 + ..., а при |x|> 1он резко расходится, и, однако же, сама функция всюду ведет себя безупречно.

Оказывается, что полное объяснение этим явлениям возможно лишь тогда, когда функции изучаются в области комплексных значений переменного х, охватывающей как действительные, так и мнимые его значения. Например, ряд для функции 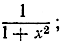должен расходиться при x = i, так как знаменатель дроби при этом значении переменного равен нулю. Отсюда следует, что ряд должен расходиться при всех таких значениях х, что |x|>|i| = 1, поскольку можно доказать, что сходимость его для одного такого значения х повлекла бы за собой его сходимость при x = i. Таким образом, вопрос о сходимости рядов, которым полностью пренебрегали в период возникновения анализа, стал одним из главных факторов создания теории функций комплексного переменного.