§ 3. Бесконечные ряды и бесконечные произведения

1. Бесконечные ряды функций

Мы не раз уже имели случай указать, что, выражая величину s в виде "суммы бесконечного ряда"

мы не утверждаем ничего иного, кроме того, что s есть предел при возрастающем n последовательности конечных "частных сумм"

где

Таким образом, равенство (1) равносильно предельному соотношению

где s_n определено с помощью (2). Если предел (3) существует, то мы говорим, что ряд (1) сходится к значению s; напротив, если предел (3) не существует, то мы говорим, что этот ряд расходится.

Например, ряд

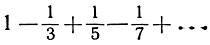
сходится к значению ^π/₄, а ряд

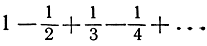
сходится к значению ln 2; но, напротив, ряд

расходится, так как частные суммы здесь равны поочередно то 1, то 0; а ряд

расходится по той причине, что частные суммы стремятся к бесконечности. Нам приходилось уже встречаться с рядами, общий член которых есть функция переменной х, имеющая вид

причем с_i не зависит от х. Такие ряды называются степенными; для них частными суммами являются многочлены

прибавление постоянного члена с₀ потребует лишь несущественного изменения обозначений в формуле (2).

Разложение функции f(x) в степенной ряд

есть, таким образом, один из способов представить функцию f(x) приближенно с помощью простейших функций - полиномов. Подводя итоги предыдущим результатам и несколько дополняя их, составим следующий список уже известных нам разложений в степенные ряды:

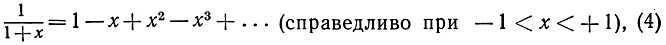
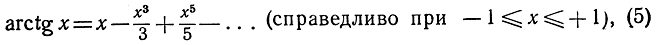
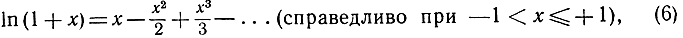
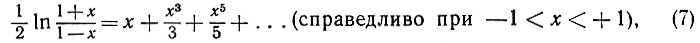
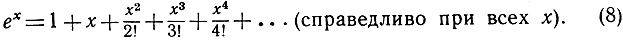
Сюда же мы присоединим еще два важных разложения

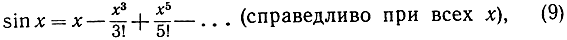
Доказательство этих разложений может быть построено как простое следствие из соотношений (см. стр. 475):

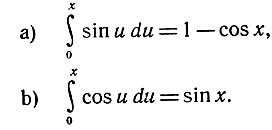
Мы отправляемся от следующего очевидного неравенства:

Интегрируя от 0 до х, где х есть некоторое фиксированное положительное число, мы находим по формуле (13) со стр. 447:

интегрируя это еще раз, получим:

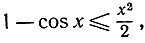
что равносильно

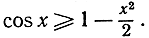
Проинтегрировав последнее неравенство, найдем:

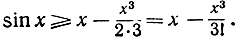
Продолжая таким же способом до бесконечности, мы получаем две серии неравенств:

Установим теперь, что при неограниченном возрастании n имеет место х_n соотношение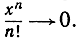

Для того чтобы это доказать, выберем некоторое фиксированное число m, такое, что 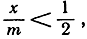и введем обозначение 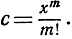Любое целое n>m представим в виде суммы n = m + r; тогда

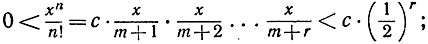
так как из того, что n→∞, следует, что r→∞, то 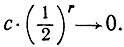Отсюда и вытекает, что справедливы тождества

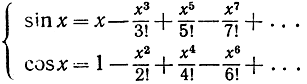
Поскольку члены этих рядов, меняя поочередно знаки, убывают по величине (по крайней мере, при |х|≤1), то ошибка, совершаемые при обрывании каждого из рядов на некотором члене, не превышают по абсолютной величине первого из отброшенных членов.

Эти ряды можно использовать при составлении таблиц.

Пример. Чему равен sin 1°? 1° равен в радианном измерении числу 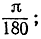следовательно,

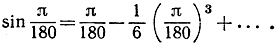
Если ограничиться выписанными двумя членами, то совершаемая при этом ошибка не будет превышать числа 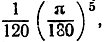которое меньше, чем 0,00000000002. Итак, sin 1° ≈ 0,0174524064, с 10 десятичными знаками.

Наконец, упомянем без доказательства о "биномиальном ряде"

где C^a_s - "биномиальный коэффициент"

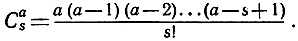
Если а = n есть целое положительное число, то С^a_n = 1, и в формуле (11) все коэффициенты C^a_s при s>n обращаются в нуль, так что мы просто получаем конечную формулу обыкновенной биномиальной теоремы. Одно из крупных открытий Ньютона, сделанных им в начале его деятельности, заключалось в том, что он обобщил биномиальную теорему на случай всех возможных значений показателя а как положительных, так и отрицательных, как рациональных, так и иррациональных. Если а не есть целое положительное число, то правая часть формулы (11) дает бесконечный ряд, сходящийся к значению, равному левой части при -1<х<+1. Если же |х|>1, то ряд (11) расходится, и знак равенства теряет всякий смысл.

В частности, подставляя в формулу (11) значение 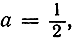мы найдем разложение

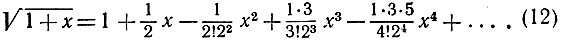
Подобно другим математикам XVIII в., Ньютон не дал настоящего доказательства своей формулы. Удовлетворительный анализ сходимости и пределы, в которых разложение оказывается справедливым, не были установлены для подобных рядов вплоть до XIX в.

Упражнение. Написать степенные ряды, в которые разлагаются функции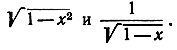

Разложения (4)-(11) являются частными случаями общей формулы Брука Тейлора (1685-1731), дающей разложение функции f (x) в степенной ряд вида

Подмечая закон, выражающий коэффициенты этого ряда с_i с помощью функции f(x) и ее производных, можно утверждать справедливость этого разложения для очень обширного класса функций.

Здесь невозможно привести строгое доказательство формулы Тейлора; невозможно также точно сформулировать условия, при которых она справедлива. Но следующие общедоступные соображения прольют некоторый свет на относящиеся сюда взаимоотношения и существенные факты.

Допустим предварительно, что разложение (13) возможно. Далее предположим, что функция f(x) дифференцируема, что ее производная f (х) дифференцируема, и так далее, так что существует бесконечная последовательность производных

Наконец будем дифференцировать бесконечный степенной ряд почленно точно так, как если бы это был конечный многочлен, не озабочиваясь вопросом о законности такой процедуры. После всех этих допущений можно определить коэффициенты с_n, зная поведение функции f(x) в окрестности точки х = 0. Прежде всего, подставляя в формулу (13) x = 0, мы находим

так как все члены ряда, содержащие переменное х, исчезают. Дифференцируя тождество (13), мы получаем

снова подставляя значение х = 0, но на этот раз в формулу (13'), мы находим

Дифференцируя (13'), мы получаем

подставляя затем в полученную формулу (13") х = 0, мы видим, что

Аналогично, продифференцировав (13") и затем подставив x = 0, получаем

и, продолжая дальше таким же образом, мы найдем общую формулу для коэффициента с_n:

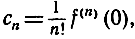
где f⁽ⁿ⁾ (0) представляет собой значение n-й производной от функции f(x) при х = 0. В результате получим ряд Тейлора:

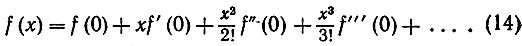
Пусть читатель в качестве упражнения проверит/что в примерах (4)-(11) коэффициенты степенных рядов составлены как раз по этому закону.