
2. Порядок возрастания функции ln(n!)
Во многих приложениях, например в теории вероятностей, важно знать порядок возрастания или "асимптотическое поведение" выражения n! при очень больших значениях n. Займемся здесь изучением логарифма от n!, т. е. выражения
Рn = ln 2 + ln 3 + ...+ ln n.
Мы покажем, что в качестве "асимптотического значения" выражения Рn может служить произведение n ln n, т. е. что
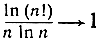
при n→∞.
Проведем доказательство так, как это обыкновенно делается, когда нужно сравнить сумму с интегралом. На рис. 287 сумма Рn равна сумме площадей прямоугольников, верхние стороны которых обозначены сплошными линиями и общая площадь которых не превосходит площади
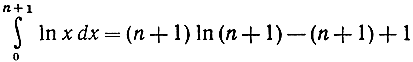
в пределах от 1 до n + 1 под логарифмической кривой [см. стр. 548, упражнение (а)]. Но в то же самое время сумма Рn равна сумме площадей прямоугольников, верхние стороны которых обозначены пунктиром и общая площадь которых превосходит площадь под той же кривой в пределах от 1 до n;
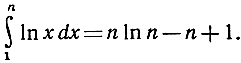
Отсюда мы имеем:
n ln n - n + 1<Pn<(n+1)ln(n+1) - n;
разделив это неравенство на n ln n, получим:
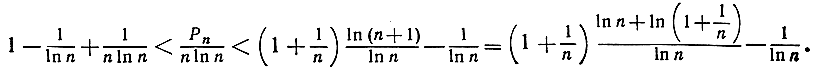
Очевидно, и верхняя и нижняя границы, между которыми заключено Р отношение 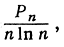 стремятся к единице, и таким образом наше утверждение доказано.
стремятся к единице, и таким образом наше утверждение доказано.
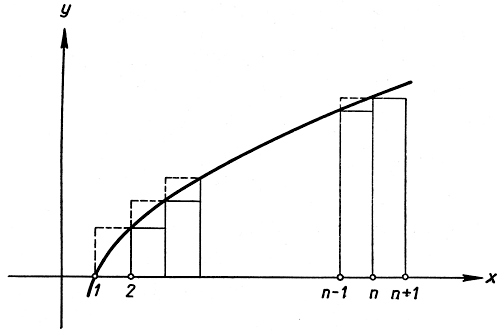
Рис. 287. Оценка ln (n!)
Упражнение. Доказать, что упомянутые выше границы соответственно больше 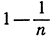 и меньше
и меньше 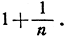
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'