§ 2. Порядки возрастания

1. Показательная функция и степени переменного х

В математике мы постоянно встречаемся с последовательностями чисел а_n, которые имеют бесконечный предел. Часто бывает нужно сравнить такую последовательность с другой последовательностью, например, чисел b_n, тоже стремящихся к бесконечности, но, может быть, "быстрее", чем последовательность чисел а_n. Уточним это понятие: мы скажем, что b_n стремится к бесконечности быстрее, чем а_n, или b_n имеет более высокий порядок возрастания, чем а_n, если отношение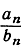 (в котором как числитель, так и знаменатель стремятся к бесконечности) стремится к нулю при возрастании n. Например, последовательность b_n = n² стремится к бесконечности быстрее, чем последовательность а_n = n, а эта последовательность в свою очередь быстрее, чем последовательность с_n = √n, так как

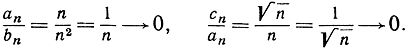
Ясно, что n^s стремится к бесконечности быстрее, чем n^r при s>r>0, так как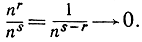

Если отношение 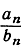стремится к некоторой конечной постоянной с, отличной от нуля, то мы говорим, что обе последовательности аn и b_n стремятся к бесконечности с одинаковой скоростью, или что они имеют одинаковый порядок возрастания. Так, например, а_n = n² и b_n = 2n² + n имеют один и тот же порядок возрастания, потому что

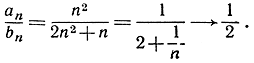
Могла бы возникнуть мысль, что возрастание любой последовательности а_n с бесконечным пределом может быть "измерено" с помощью степеней n^s так же, как любой отрезок может быть измерен с помощью линейки с делениями. Стоило бы только для этого найти подходящую степень n^s с тем же порядком возрастания, что и а_n, т. е. такую, что отношение ^a_n/_n^s стремится к некоторой конечной, отличной от нуля постоянной. Но совершенно замечательным является то обстоятельство, что осуществить это отнюдь не всегда возможно - хотя бы потому, что показательная функция аⁿ при а>1 (например, еⁿ) стремится к бесконечности быстрее, чем какая бы то ни было степень n^s, как бы велик ни был показатель s; с другой стороны, функция ln n стремится к бесконечности медленнее, чем какая бы то ни было степень n^s, как бы мал ни был положительный показатель s. Другими словами, мы имеем соотношения

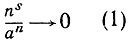
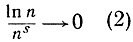
при n→∞. Заметим, что показатель степени s - не обязательно целое число; он может быть любым фиксированным положительным числом.

Для того чтобы доказать соотношение (1), мы упростим наше утверждение тем, что извлечем из соотношения (1) корень степени s; ясно, что вместе с корнем стремится к нулю и подкоренное выражение. Итак, нам остается только доказать, что

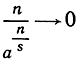
при возрастании n. Пусть 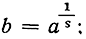так как по предположению а больше единицы, то и b и 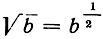также больше 1. Можно написать

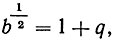
где q положительно. Теперь, в силу неравенства (6) на стр. 39,

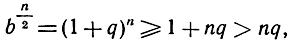
так что

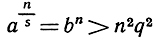
и, следовательно,

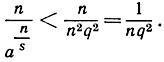
Так как выражение справа стремится к нулю при n→∞, доказательство закончено.

Нужно заметить, что соотношение

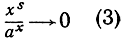
остается в силе, когда х стремится к бесконечности любым способом, пробегая последовательность х₁, х₂, ..., которая может и не совпадать с последовательностью 1, 2, 3, ... целых положительных чисел. В самом деле, при пn-1≤х≤n мы имеем

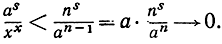
Это замечание можно использовать для доказательства соотношения (2). Если положить х = ln n и e^s = а, так что n^s = (e^s)^x, то дробь в левой части (2) примет вид

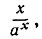
и мы приходим к выражению, имеющемуся в соотношении (3) при s = 1.

Упражнения.

1. Доказать, что при х→∞ функция ln ln x стремится к бесконечности медленнее, чем ln х.
2. Производная от функции 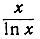равна разности 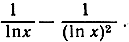Доказать, что при возрастании х производная "асимптотически равна" первому члену, 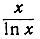т. е. что отношение упомянутых величин при х→∞ стремится к 1.