3. Другие приложения понятия интеграла. Работа. Длина кривой

Оторвав аналитическое представление интеграла от его первоначальной геометрической интерпретации, мы встречаемся с целым рядом других, не менее важных интерпретаций и приложений этого основного понятия. Например, в механике интеграл может быть интерпретирован как выражение работы. Достаточно будет разъяснить это на следующем простом примере. Предположим, что некоторая масса движется по оси х под влиянием силы, направленной вдоль этой оси. Будем считать, что вся масса сосредоточена в одной точке с координатой х и что сила задана как функция этой точки f(x), причем знак функции f(x) указывает на направление силы. Если сила постоянна и передвигает массу из точки а в точку b, то работа, произведенная ею, равна произведению величины силы f на пройденный массой путь: (b-a)f. Но если сила меняется вместе с изменением х, то придется определять общую произведенную работу с помощью предельного процесса (подобно тому, как мы прежде определяли скорость). Для этой цели мы разобьем промежуток от а до b, как и прежде, на мелкие частные промежутки точками х₀ = а, х₁, x₂,..., х_n = b; затем предположим, что в каждом частном промежутке сила остается постоянной и равной, скажем, величине f(x_v), истинному значению силы в конечной точке, и вычислим работу, соответствующую такой "ступенчатой" силе:

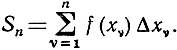
Если мы теперь, как раньше, станем уменьшать промежутки деления, заставляя n неограниченно расти, мы увидим, что сумма будет стремиться к интегралу

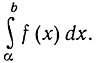
Таким образом, работа, совершаемая непрерывно меняющейся силой, определена с помощью интеграла.

В частности, рассмотрим массу m, связанную с началом координат х = 0 упругой пружиной. Сила f(x), согласно рассуждению на стр. 498, будет пропорциональна х

где k² - положительная постоянная. Тогда работа, совершенная этой силой при перемещении массы m из начала координат в точку b, выразится интегралом

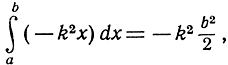
а работа, которую мы сами должны затратить при растяжении пружины до точки b, равна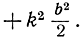

Другое приложение общего понятия интеграла - это вычисление длины дуги кривой. Предположим, что рассматриваемая часть кривой представлена функцией y = f(x), производная которой 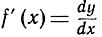также непрерывная функция. Для того чтобы определить длину, мы будем действовать точно так, как если бы нам надо было измерить длину кривой для практических целей при помощи линейки с делениями. Впишем в дугу АВ ломаную линию с n маленькими сторонами, измерим общую длину (периметр) L_n этой ломаной и станем рассматривать эту длину как некоторое приближение; заставим n возрастать, а наибольшую из сторон ломаной - стремиться к нулю; тогда мы получим в качестве длины дуги АВ следующий предел:

(В главе VI этим же способом была получена длина окружности как предел периметра вписанного правильного n-угольника.) Можно доказать, что для достаточно гладких кривых этот предел существует и не зависит от того, каким образом выбирается последовательность вписанных ломаных. Те кривые, для которых это имеет место, называются спрямляемыми. Всякая "порядочная" кривая, встречающаяся в теории или ее приложениях, оказывается спрямляемой, и мы не станем углубляться в исследование "патологических" случаев. Достаточно будет показать, что дуга АВ для функции y = f(x) с непрерывной производной f'(x) имеет длину L в указанном смысле и что длина L может быть выражена с помощью интеграла.

С этой целью обозначим абсциссы точек А и В соответственно через а и b, затем разобьем промежуток от а до b, как и прежде, точками а = х₀, x₁, х₂, ... , x_j, ... , x_n = b с разностями Δx_j = x_j - x_j-1 и рассмотрим ломаную линию с вершинами (х₁, y₁ = f(x_j)), расположенными над точками деления. Длина одной из сторон ломаной выразится формулой

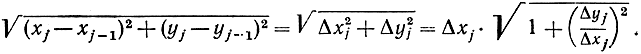
Отсюда для общей длины ломаной линии получается выражение

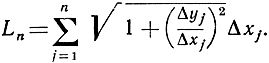
Если заставить теперь n стремиться к бесконечности, то разностное отношение 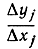будет стремиться к производной 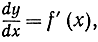и мы получим для длины L интегральное выражение

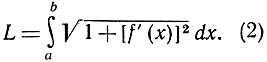
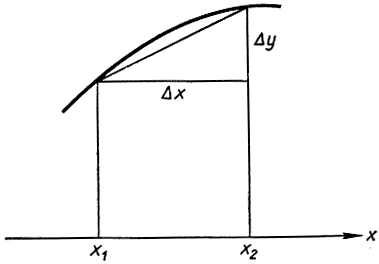
Рис. 286. К определению длины дуги

Не вдаваясь в дальнейшие подробности этих теоретических рассуждений, сделаем два дополнительных замечания. Во-первых, если точку В считать подвижной точкой на данной кривой с абсциссой х, то L = L(x) становится функцией переменного х, и согласно основной теореме мы имеем формулу

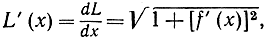
которую часто приходится применять. Во-вторых, хотя формула (2) и дает "общее" решение задачи нахождения длины дуги, все же она редко позволяет найти явное выражение этой длины в отдельных частных случаях. В самом деле, чтобы получить числовое значение длины дуги, мы должны подставить данную функцию f(x), или, точнее, f'(x), в формулу (2) и тогда осуществить фактическое интегрирование полученного выражения. Но здесь возникают, вообще говоря, непреодолимые трудности, если мы ограничим себя областью элементарных функций, рассмотренных в этой книге. Укажем небольшое число случаев, для которых интегрирование возможно. Функция

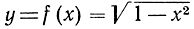
имеет графиком единичный круг; для нее мы получаем

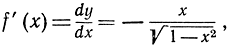
откуда

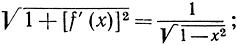
следовательно, длина дуги окружности выражается интегралом

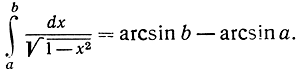
Для случая параболы y = х² мы имеем f'(x) = 2х, а длина дуги от х = 0 до х = b равна

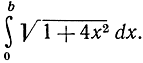
Для кривой y = ln sin x мы имеем f'(x) = ctg x, и длина дуги выражается интегралом

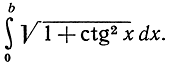
Мы удовольствуемся лишь простым написанием этих интегральных выражений. Их можно было бы вычислить, применяя несколько более развитую технику интегрирования, чем та, которая имеется в нашем распоряжении, но мы не пойдем дальше в этом направлении.