2. Интеграл

Аналогично и положение с интегралом от непрерывной функции f(x). Вместо того чтобы "площадь под кривой" принимать как величину, объективно существующую и которую a posteriori можно выразить с помощью предела последовательности конечных сумм, этот предел в анализе принимают в качестве определения интеграла. Эта концепция интеграла образует первичную основу, из которой затем выводится понятие площади. Мы вынуждены стать на эту точку зрения вследствие сознания того, что геометрическая интуиция обладает известной расплывчатостью, когда она применяется к таким общим аналитическим понятиям, как непрерывная функция. Мы начнем с построения суммы

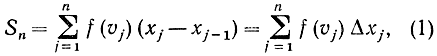
где х₀ = а, х₁, ..., х_n = b - точки деления промежутка интегрирования, Δx_j = х_j - x_j-1 - приращение переменной х, или длина j-го частного промежутка, а υ_j - произвольное значение переменного х в этом частном промежутке, т. е. x_j-1≤υ_j≤х_j (мы можем взять, например, υ_j = x_j или υ_j = x_j-1).

Далее, мы образуем последовательность подобных сумм, в которых число n частных промежутков возрастает, причем длина минимального частного промежутка стремится к нулю. Тогда справедливо следующее основное положение: сумма S_n, составленная для данной непрерывной функции f(x), стремится к некоторому определенному пределу А, не зависящему от способа разбиения промежутка интегрирования и от выбора точек υ_j. По определению этот предел есть интеграл 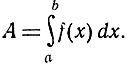Конечно, существование этого предела должно быть аналитически доказано, если мы не хотим ссылаться на интуитивное геометрическое представление площади. Это доказательство приводится в каждом руководстве анализа, учитывающем требования математической строгости.

Сравнение дифференцирования и интегрирования приводит нас к следующему противопоставлению. Свойство дифференцируемости, несомненно, налагает ограничительное условие на класс всех непрерывных функций; вместе с тем фактическое выполнение операции дифференцирования сводится на практике к процедурам, основанным лишь на нескольких простых правилах. В противоположность этому каждая непрерывная функция без исключения интегрируема, так как обладает интегралом между любыми двумя данными пределами. Однако прямое вычисление интегралов, понимаемых как пределы сумм, даже в случае самых простых функций, вообще говоря, дело очень трудное. Но тут-то и оказывается, что основная теорема анализа во многих случаях становится решающим орудием при осуществлении интегрирования. И все же для большей части функций, в том числе даже для некоторых совершенно элементарных, интегрирование не дает простых явных выражений, и числовые выкладки для интегралов требуют более продвинутых методов.