1. Дифференцируемость

Понятие производной от некоторой функции y = f(x) мы связывали с интуитивным представлением о касательной к графику этой функции. Но так как общая концепция функции чрезвычайно широка, то в интересах логической законченности необходимо уничтожить эту зависимость от геометрической интуиции. В самом деле, мы ведь не гарантированы от того, что интуитивные свойства, бросающиеся в глаза при рассмотрении простых кривых, подобных кругу или эллипсу, не исчезнут для графиков более сложных функций. Рассмотрим, например, функцию, изображенную на рис. 282, график которой имеет угловую точку.

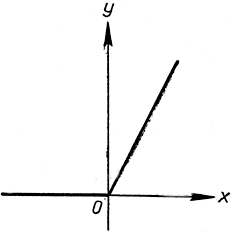
Рис. 282. y = х + |х|

Эта функция определяется уравнением y = х + |х|, где символом |х| обозначается абсолютная величина х; иными словами,

Другим примером такого рода может служить функция y = |х|, а также функция y = x + |x| + (х-1) + |х - 1|. Графики этих функций в некоторых точках перестают иметь определенную касательную, т. е. определенное направление; это значит, что функция в соответствующих точках х не имеет производной.

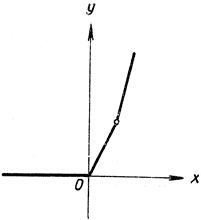
Рис. 284. y = х + |х| + (x-1) + |x-1|

Упражнения.

1. Построить (т. е. записать с помощью конкретных аналитических выражений) функцию f (x), график которой есть половина правильного шестиугольника.
2. Где расположены угловые точки графика
   
   
   Каковы точки разрыва производной f' (х)?

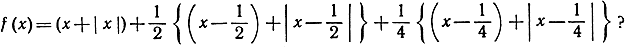
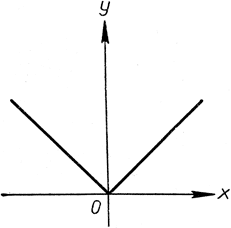
Рис. 283. y = |х|

В качестве простого примера недифференцируемости уже иного типа приведем функцию

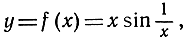
получаемую посредством умножения функции sin ¹/_x (см. стр. 314) на множитель х; положим по определению, что f(x) = 0 при х = 0. Эта функция, график которой для положительных значений переменного х изображен на рис. 285, непрерывна в каждой точке. График колеблется бесконечно часто в окрестности точки х = 0, причем "волны" становятся бесконечно малыми, если мы приближаемся к нулю. Наклон этих волн дается формулой

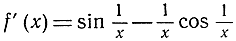
(пусть читатель проверит это в качестве упражнения); при стремлении х к нулю этот наклон колеблется между все возрастающими положительной и отрицательной границами. Мы можем сделать попытку найти производную в точке х = 0, переходя к пределу при h→0 в разностном отношении

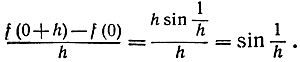
Но при h→0 это разностное отношение колеблется между -1 и +1 и не стремится ни к какому пределу; следовательно, функция не может быть продифференцирована в точке х = 0.

">
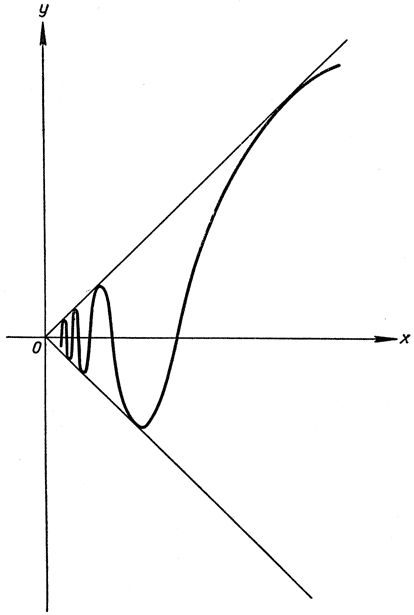Рис. 285.

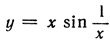
Эти примеры указывают на трудности, внутренне присущие самому вопросу. Вейерштрасс удивительно ярко иллюстрировал положение вещей, построив непрерывную функцию, график которой не имеет производной ни в одной точке. В то время как дифференцируемость влечет за собой непрерывность, непрерывность, как показывает этот пример, отнюдь не влечет за собой дифференцируемости; в самом деле, функция Вейерштрасса всюду непрерывна, а вместе с тем нигде не дифференцируема. На практике трудности такого рода не встретятся. Обычно встречающиеся кривые являются "гладкими" (за исключением разве только отдельных изолированных точек), т.е. дифференцирование не только возможно, но даже сама производная является непрерывной. Что же в таком случае может нам помешать просто сделать оговорку, что никакие "патологические" явления не будут фигурировать в задачах, подлежащих нашему рассмотрению? Именно так и поступают в анализе те, кому приходится иметь дело только с дифференцируемыми функциями. В главе VIII мы провели дифференцирование обширного класса функций и тем самым доказали их дифференцируемость.

Поскольку дифференцируемость функции не есть логическая неизбежность, она - с математической точки зрения - должна быть или постулирована или доказана. В таком случае само понятие о касательной или о направлении кривой (первоначальный источник идеи производной) ставится в зависимость от чисто аналитического определения производной: если функция y = f(x) дифференцируема, т. е. если разностное отношение 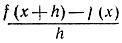имеет единственный предел f' (x) при стремлении h к нулю с обеих сторон, то принято говорить, что соответствующая кривая имеет касательную с наклоном f'(x). Таким образом, наивная позиция Ферма, Лейбница и Ньютона в современном анализе вывернута наоборот - в интересах логической стройности.

Упражнения.

1. Показать, что непрерывная функция, определенная формулой 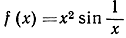и добавочным условием f (0) = 0, дифференцируема в точке х = 0.
2. Показать, что функция разрывна при х = 0, что функция 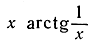непрерывна в этой точке, но не имеет в ней производной и что функция 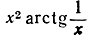дифференцируема при х = 0. (В двух последних примерах следует положить значение функций при х = 0 равным нулю.)