3. Другие примеры. Простые колебания

Показательная функция встречается часто в более сложных комбинациях. Например, функция

где k - положительная константа, является решением дифференциального уравнения

Функция (8) играет большую роль в теории вероятностей и в статистике, выражая, как говорят, "нормальный" закон распределения.

Тригонометрические функции u = cos t и u = sin t также удовлетворяют простому дифференциальному уравнению. Прежде всего обратим внимание на соотношения

образующие "систему двух дифференциальных уравнений с двумя неизвестными функциями". Дифференцируя вторично, мы находим

таким образом, обе функции u и v временного переменного t могут рассматриваться как решение одного и того же дифференциального уравнения

Это - очень простое дифференциальное уравнение "второго порядка", т. е. уравнение, содержащее вторую производную от функции z. Оно, или, лучше сказать, его обобщение, содержащее положительную постоянную k²,

(решениями которого являются функции z = cos kt и z = sin kt), постоянно встречается при изучении теории колебаний, и потому "синусоидальные" кривые u = sin kt и v = cos kt (рис. 280) в высшей степени интересуют всех, кто занимается конструкцией механизмов, совершающих или порождающих колебательные движения.

Следует заметить, что дифференциальное уравнение (10) представляет "идеальный" случай, когда трение или сопротивление предполагается отсутствующими.

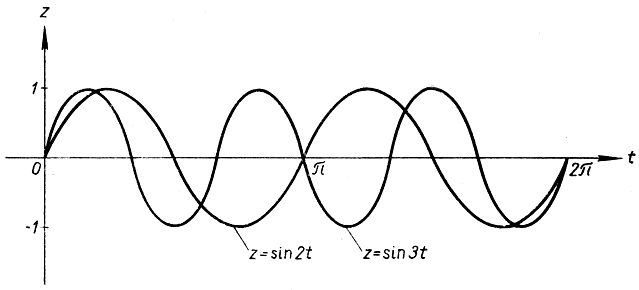
Рис. 280. Гармонические колебания

В дифференциальном уравнении колебательного движения сопротивление выражается лишним членом, а именно rz', так что уравнение имеет вид"

его решениями являются "затухающие" колебания, выражающиеся математически с помощью формулы

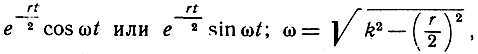
что графически представлено на рис. 281. (В качестве упражнения читатель пусть проверит правильность этих решений путем дифференцирования.) Затухающие колебания того же самого типа, что и обыкновенные синусоиды или косинусоиды, но с течением времени их размах уменьшается вследствие присутствия показательного множителя, убывающего более или менее быстро, в зависимости от величины коэффициента трения r.

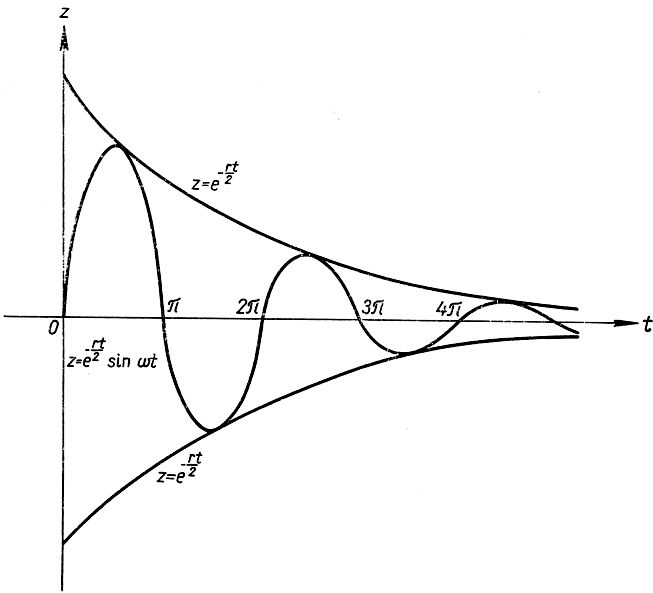
Рис. 281. Затухающие колебания