2. Дифференциальное уравнение показательной функции. Радиоактивный распад. Закон роста. Сложные проценты

Показательная функция u = е^х является решением дифференциального уравнения

так как производная от показательной функции равна, самой показательной функции. Вообще, функция u = се^х, еде с - произвольное постоянное, есть решение уравнения (1). Аналогично, функция

где с и k - две какие-нибудь постоянные, есть решение дифференциального уравнения

Обратно, всякая функция u = f(x), удовлетворяющая уравнению (3), имеет вид (2). В самом деле, пусть функции x = h(u) и u = f(x) взаимно обратные; в таком случае, следуя правилам дифференцирования обратной функции, найдем:

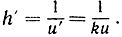
Функцией, первообразной по отношению к найденной производной 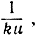является функция 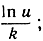итак, 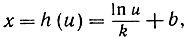где b - некоторое постоянное. Отсюда

и

Полагая постоянную величину е^-bk равной с, получим

как и нужно было предвидеть.

Большое значение уравнения (3) заключается в том, что оно "регулирует" физические процессы, в которых количество и какого-нибудь вещества представляет собой функцию времени

и притом изменяется таким образом, что скорость изменения в каждый момент пропорциональна количеству и вещества, имеющегося налицо. В этом случае скорость изменения в момент t, т. е.

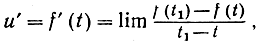
равна ku, где k - постоянный коэффициент пропорциональности, положительный, если и возрастает, и отрицательный, если и убывает. В обоих случаях функция u удовлетворяет дифференциальному уравнению (3); следовательно, она имеет вид

Постоянная с определена, если известно количество вещества u₀, имевшееся налицо в начальный момент, т. е. при t = 0. Величину u₀ мы должны получить при подстановке t = 0 в уравнение (2):

отсюда и получается

Следует обратить внимание на то, что мы исходим из предположения, что задана скорость изменения величины u, и выводим закон (4), который позволяет вычислить фактическое количество вещества u в любой момент времени t. Эта задача как раз противоположна задаче нахождения производной от какой-нибудь функции.

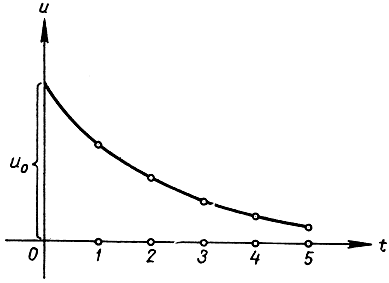
Рис. 279. Убывание по экспоненциальному закону: u = u₀e^kt, <0

Типичным примером явления указанного типа можно считать распад некоторого радиоактивного вещества. Пусть u = f(t) есть количество вещества в момент времени t; если принять гипотезу, что каждая индивидуальная частица вещества имеет некоторую определенную вероятность распада и что эта вероятность не зависит от присутствия других частиц, то скорость, с которой количество u будет распадаться в данный момент времени t, будет пропорциональна общему количеству вещества u, имеющемуся налицо. Таким образом, функция u должна удовлетворять уравнению (3) при отрицательной постоянной k, которая измеряет быстроту процесса распада; итак, вид функции следующий:

Отсюда вытекает, что в равные промежутки времени подвергается распаду одна и та же доля имеющегося налицо вещества; действительно, если u₁ есть количество вещества, имеющегося в момент времени t₁, а u₂ - в некоторый последующий момент времени t₂, то

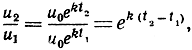
и последнее выражение зависит только от разности t₂-t₁. Вычислим, например, сколько времени потребуется для того, чтобы в процессе распада осталась ровно половина вещества: нам нужно определить s = t₂-t₁ из уравнения

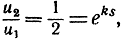
и мы получаем

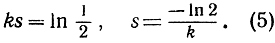
Напротив, зная s, можно определить k:

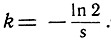
Для каждого радиоактивного вещества значение s носит название "периода полураспада". Число s или некоторое аналогичное (например, такое, как значение r, при котором 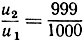может быть найдено экспериментальным путем. Для радия период полураспада равен приблизительно 1550 годам и, следовательно,

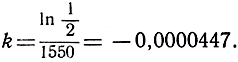
Отсюда мы находим, что

Примером закона, близкого к рассмотренному только что закону показательной функции, может служить закон так называемых сложных процентов. Пусть некоторый капитал u₀ (долларов) отдан в рост из расчета 3 % (сложных) в год. По истечении одного года капитал станет равным

по истечении двух лет он будет

наконец, по истечении t лет он выразится числом

Теперь, если начисление процентов происходило бы не один раз в год, а один раз в месяц, или, вообще, один раз в n-ю часть года, то по истечении t лет наращенный капитал выразился бы формулой

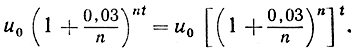
Если предположить, что число n очень велико, так что проценты присчитываются ежедневно или даже ежечасно, то, воображая, что n стремится к бесконечности, мы заметим, что величина, стоящая в скобках, стремится к е^0'03 согласно сказанному в § 6 и в пределе капитал но истечении t лет выразится формулой

что соответствует процессу непрерывного присчитывания сложных процентов. Можно также вычислить время s, нужное для того, чтобы удвоить основной капитал, отданный в рост по 3 сложных непрерывно начисляемых процента. Мы имеем 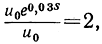откуда 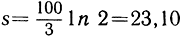Итак, капитал удвоился бы по истечении приблизительно 23 лет.

Вместо того чтобы шаг за шагом проделывать описанную выше процедуру и затем переходить к пределу, мы могли бы получить формулу (7), просто сказав, что скорость u' возрастания капитала и пропорциональна этому капиталу, с коэффициентом пропорциональности k = 0,03, согласно дифференциальному уравнению

Тогда формула (7) вытекала бы непосредственно из общей формулы (4).