§ 7. Дифференциальные уравнения

1. Определения

Главенствующая роль, которую показательные и тригонометрические функции играют в математическом анализе и его применениях к задачам физики, основывается на том, что эти функции являются решениями простейших "дифференциальных уравнений".

Дифференциальным уравнением относительно неизвестной функции u = f(x) с производной u' = f' (x) (обозначение u' очень удачно сокращает обозначение f' (x), поскольку величина и и ее формальная зависимость от х как функции f (х) не нуждаются в особенном подчеркивании) называется уравнение, содержащее функцию u, производную u' и, может быть, независимое переменное х, как например

или

В более общем случае дифференциальное уравнение может содержать вторую производную u" = f" (x) или производные более высокого порядка, как например уравнение

Во всех подобных случаях задачей является нахождение функции u = f (х), удовлетворяющей данному уравнению.

Решение дифференциальных уравнений есть широкое обобщение задачи интегрирования, понимаемой как нахождение первообразной функции по заданной функции g (x): последнее сводится к решению простейшего дифференциального уравнения

Например, решениями дифференциального уравнения

являются функции 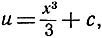где с - произвольное постоянное.