5. Бесконечный ряд для логарифма. Вычисление логарифмов

Числовые значения логарифмов вычисляются отнюдь не с помощью формулы (15). Гораздо лучше приспособлено для этой цели совершенно иное, более полезное, явное выражение, имеющее, кроме того, большое теоретическое значение. С помощью метода, примененного на стр. 477 при вычислении π, мы получим это выражение, опираясь на определение логарифма по формуле (1). Но здесь необходим один предварительный шаг: вместо функции ln x рассмотрим функцию y = ln (1+х), составленную из функций y = ln z и z = 1 + х. Имеем:

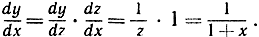
Итак, функция ln (1+х) является первообразной по отношению к функции 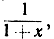и мы заключаем согласно основной теореме, что интеграл от функции 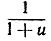в пределах от 0 до х равен выражению ln (1+х) - ln 1 = ln (1+х), или, в символической записи,

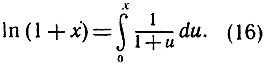
(Эту формулу можно было бы, конечно, получить и интуитивно из геометрической интерпретации логарифма как площади. Сравните с рассуждением на стр. 479.)

В формулу (16) подставим вместо (1+u)¹ сумму геометрической прогрессии, как мы это делали на стр. 477, а именно

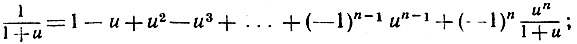
из осторожности мы предпочитаем оперировать не с бесконечным рядом, а с конечной суммой и остаточным членом, который равен

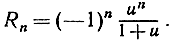
Подставив эту сумму в формулу (16), можно применить правило почленного интегрирования конечной суммы. Интеграл от степени u^s в пределах от 0 до х равен 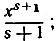таким образом, мы получим немедленно

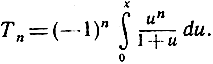
где остаточный член Т выражается интегралом

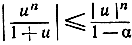
Покажем теперь, что Т_n стремится к нулю при возрастании n, предварительно условившись, что переменное х может быть лишь больше -1 и не превышать +1, т. е., другими словами, что выполнено неравенство

(заметим, что х = +1 включается, в то время как х = - 1 не включается). Согласно нашему предположению, в промежутке интегрирования переменное и больше, чем некоторое число -а, которое может быть близко к - 1, но во всяком случае больше, чем -1, так что -1<-α<u. Отсюда следует 0<1-α<1+u. Поэтому при условии, что и заключено в промежутке от 0 до х, имеет место неравенство

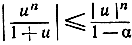
и, следовательно,

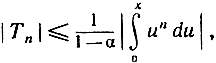
или

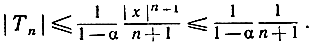
Поскольку число 1-α является постоянным, мы видим, что выражение, стоящее справа, а следовательно, и стоящее слева |Т_n|, при возрастании n стремится к нулю; значит, из неравенства

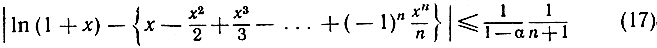
вытекает, что при -1<х<1 справедливо равенство

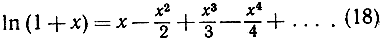
Подставляя, в частности, х = 1, получаем любопытную формулу

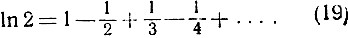
Эта формула по своей структуре похожа на выведенную раньше формулу, представляющую в виде ряда число ^π/₄.

Ряд (18) не имеет большого практического значения для вычисления логарифмов, потому что область изменения величины 1 + х ограничена промежутком от 0 до 2, а также по той причине, что сходимость ряда очень медленная: пришлось бы брать много членов, чтобы получить сколько-нибудь точный результат. При помощи следующего приема мы получим выражение, практически более удобное. Вместо х в формулу (18) подставим - х:

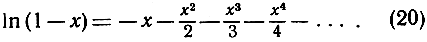
Вычитая, далее, формулу (20) из формулы (18) и применяя преобразование 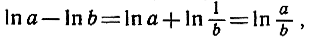мы получим:

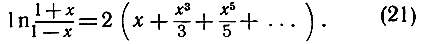
Этот ряд сходится быстрее, и, кроме того, левая часть формулы может теперь выразить логарифм любого положительного числа z, так как уравнение 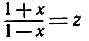имеет при любом положительном z решение х, заключенное между -1 и +1. Например, если нам нужно вычислить ln 3, то мы положим 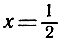и тогда'получим

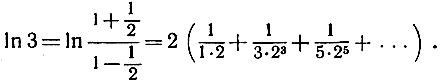
Взяв всего лишь 6 членов, вплоть до члена 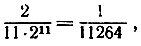мы находим значение

с пятью значащими цифрами.