4. Явные выражения числа е и функций е^х и ln х в виде пределов

Для того чтобы найти явные формулы, выражающие эти функции, мы используем формулы дифференцирования показательной и логарифмической функций. Так как производная функции ln x равна ¹/_x, то в силу определения производной мы получаем соотношение

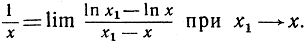
Положим х₁ = х + h и допустим, что h стремится к нулю, пробегая последовательность 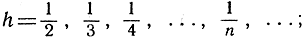тогда' применяя правила действий с логарифмами, мы получим:

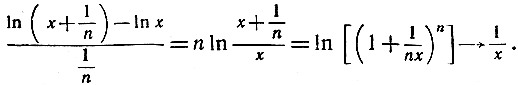
Если вместо ¹/_x мы подставим z и перейдем к пределу, то написанное выше соотношение примет вид:

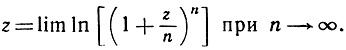
Или, в терминах показательной функции:

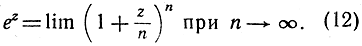
Мы получили общеизвестную формулу, определяющую показательную функцию просто как предел. В частности, при z = 1 эта формула дает

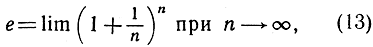
а при z = - 1 получается

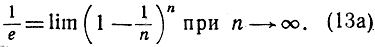
Эти выражения сразу ведут к разложениям в бесконечные ряды. По биномиальной теореме, можно написать

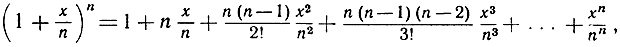
или

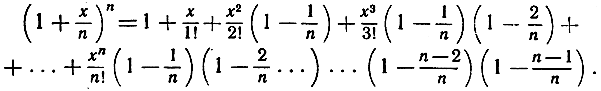
Позволительно догадываться и нетрудно полностью доказать (подробности мы здесь опускаем), что можно перейти к пределу при n→∞ путем замены в каждом члене величины ¹/_n на 0. Это дает хорошо известный бесконечный ряд, который служит для вычисления функции е^х:

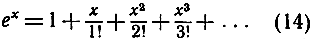
и, в частности, при х = 1 ряд, сходящийся к пределу е:

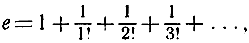
чем устанавливается идентичность е с тем числом, определение которого дано на стр. 330. При х = - 1 получается ряд

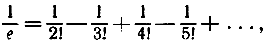
который дает превосходное приближение уже при очень малом числе членов, так как ошибка, которую мы совершаем, обрывая ряд на n-м члене, меньше величины (n + 1)-го члена.

Пользуясь формулой дифференцирования показательной функции, можно получить интересное выражение для логарифма. Имеет место соотношение

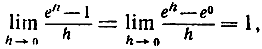
так как указанный предел есть не что иное, как значение производной от функции е^y при y = 0, а таковое равно 1. Подставим в эту формулу вместо h значение 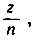, где z - произвольное число, а n пробегает последовательность целых положительных чисел. Тогда мы получим

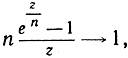
или

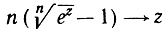
при n→∞. Вводя обозначение z = ln x, или е^z = x, можно окончательно написать:

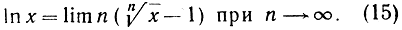
Поскольку 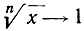при n→∞ (см. стр. 357), формула (15) представляет логарифм в виде произведения двух множителей, из которых первый стремится к бесконечности, а второй - к нулю.

Примеры и упражнения

Введение показательной и логарифмической функций дает возможность оперировать с функциями достаточно обширного класса и открывает доступ ко многим приложениям.

Продифференцировать:

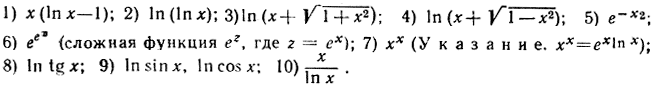
Найти максимумы и минимумы функций: 11) xe^-x; 12)x²e^-x; 13)xe^-ax.

^* 14) Найти геометрическое место максимумов кривой y = хе^-ах при переменном параметре а.

15) Показать, что все последовательные производные от функции е^-х2 имеют вид произведения множителя е^-х2 на многочлены от х последовательно возрастающих степеней.

^* 16) Показать, что производные n-го порядка от функции 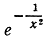имеют вид произведения множителей 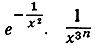на многочлен степени 2n-2.

^* 17) Логарифмическое дифференцирование. Дифференцирование произведений может быть иногда упрощено путем применения основного свойства логарифма. Действительно, имея дело с произведением

можно написать

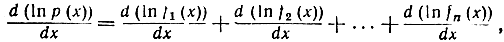
и дальше, с помощью формулы дифференцирования сложных функций, отсюда следует:

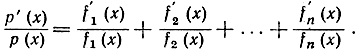
Воспользоваться этим при дифференцировании примеров