3. Формулы дифференцирования функций е^х, а^х, x^s

Так как показательную функцию мы определили как обратную по отношению к функции y = ln х, то из правила дифференцирования обратных функций (§ 3) вытекает, что

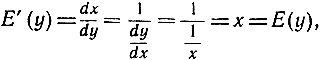
т. е.

Производная от "натуральной" показательной функции тождественно равна самой функции. Это есть истинный источник всех свойств показательной функции и основная причина ее роли во всех приложениях, как это станет видно в последующих разделах. Используя дифференциальные обозначения, мы можем записать формулу (11) в следующем виде:

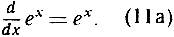
В более общем случае, дифференцируя сложную функцию

с помощью правила, данного в § 3, мы получим равенство

Таким образом, полагая α = ln a, мы найдем, что функция

имеет производную

Переходя теперь к рассмотрению степенной функции

при любом действительном показателе s и при положительном переменном х, мы можем определить ее по формуле

Снова применяя правило дифференцирования сложной функции к случаю, когда f (х) = e^sz, z = ln x, мы найдем производную

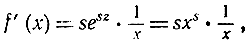
так что

в полном соответствии с прежним правилом дифференцирования степенной функции при рациональном показателе s.