2. Показательная (экспоненциальная) функция

Суммируя наши предыдущие результаты, мы можем сказать, что функция F (х) = ln x равна нулю при х = 1; монотонно возрастает до бесконечности при х→∞ (но при этом график имеет убывающий наклон, равный величине ¹/_x); при значениях х, меньших единицы, выражается при помощи функции 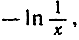так что ln x стремится к отрицательной бесконечности при х → 0.

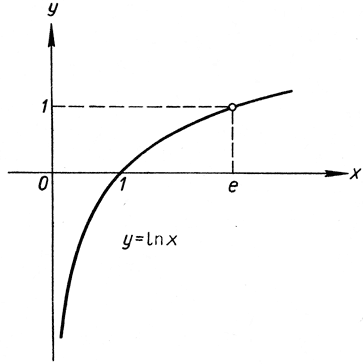
Рис. 277. y = ln x

Монотонный характер возрастания функции y = ln x позволяет рассматривать обратную ей функцию

график которой (рис. 278) получается обычным путем из графика функции y = ln х (рис. 277); эта обратная функция определена при всех значениях y от -∞ до +∞. При y→-∞ функция Е(y) стремится к нулю; при y→∞, с другой стороны, Е (y)→∞. Рассматриваемая функция Е обладает следующим основным свойством:

при любой паре значений а и b. Последнее тождество есть просто видоизменение формулы (3), выражающей свойство логарифма. Действительно, если мы придадим формуле (3) вид ln х + ln z = ln (xz) и затем положим

то будем иметь

а отсюда вытекает

что и требовалось доказать.

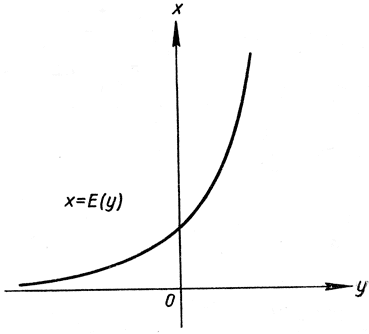
Рис. 278. х = Е(y)

Так как по определению ln е = 1, то имеет место соотношение

присоединяя к этому формулу (8), получим равенство е² = E (1)*E(1) = E (2) и т. д. Вообще,

при любом целом n. Аналогично можно получить 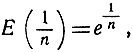так что

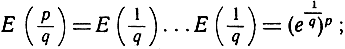
полагая затем 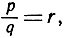заключаем, что я

при любом рациональном r. Поэтому вполне естественно определить иррациональную степень числа е по формуле

справедливой при любом действительном у, поскольку функция Е непрерывна при всех значениях y и тождественна с функцией е^y при рациональных значениях у. Формулу (8), выражающую основное свойство функции E, или, по общепринятой терминологии, экспоненциальной (показательной) функции, теперь можно выразить при помощи равенства

которое тем самым установлено для произвольных рациональных или иррациональных значений а и b.

Во всех этих рассуждениях мы относили логарифм и показательную функцию к числу е как к "основанию", точнее, к "натуральному основанию" логарифмов. Перейти от основания е к некоторому другому положительному основанию не представляет труда. Начнем с рассмотрения натурального логарифма

(что равносильно а = е^α = е^{ln α}). Показательную функцию ах мы станем определять посредством следующего сложного выражения:

Например,

Назовем функцию, обратную по отношению к функции а^х, логарифмом при основании а; нетрудно понять, что натуральный логарифм от z есть произведение х на α: другими словами, логарифм числа z при основании а получается путем деления натурального логарифма числа z на постоянный натуральный логарифм числа а. Если а = 10, то это число (с четырьмя значащими цифрами) выражается следующим образом: