1. Определение и свойства логарифма. Эйлерово число е.

Определим логарифм, или, точнее говоря, "натуральный логарифм" F (х) = ln x (его связь с обычным десятичным логарифмом будет установлена в пункте 2)

как площадь под кривой 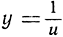пределах от u = 1 до u = х, или, что сводится к тому же, как следующий интеграл:

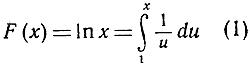
(см. рис. 5, стр. 54). Здесь переменная х может быть любым положительным числом. Нуль исключается потому, что при стремлении и к нулю функция, стоящая под интегралом, стремится к бесконечности.

Естественно заняться изучением функции F (х). Мы знаем, что первообразная функция по отношению к любой степени хⁿ представляет собой функцию того же типа, так как равна 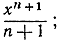исключением является степень n = -1. В этом последнем случае знаменатель n+1 превратился бы в нуль, и формула (4) на стр. 475 потеряла бы смысл. Таким образом, можно ожидать, что изучение интеграла от функции 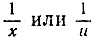приведет к новому (и интересному) типу функции.

Хотя мы и принимаем формулу (1) за определение функции log x, однако мы не "знаем" самой функции, пока мы не установим ее свойств и не найдем способов находить ее числовые значения. Нужно заметить, что для современных методов в анализе очень характерно то, что мы отправляемся от общих понятий - таких, как площадь или интеграл, и уже на основе этих понятий устанавливаем определения, подобные (1); затем выводим свойства определяемых объектов и лишь в самом конце приходим к явным выражениям, позволяющим вычислять их числовые значения.

Первое важное свойство функции In x непосредственно следует из основной теоремы § 5. Согласно этой теореме справедливо равенство

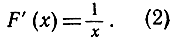
Из формулы (2) следует, что производная F (х) всегда положительна, а это указывает, очевидно, на то, что функция ln x монотонно возрастает при возрастании х.

Главное свойство логарифма выражается формулой

Значение этой формулы в практических применениях логарифмов к числовым выкладкам хорошо известно. Формулу (3) можно было бы получить интуитивно, воспользовавшись площадями, определяющими три величины, а именно: ln a, ln b и ln (ab). Но мы предпочтем развернуть доказательство, типичное для анализа: наряду с функцией F (х) = ln x, рассмотрим другую функцию

полагая ω = f (x) = ах, где а - произвольная положительная постоянная. Функцию k (х) можно легко продифференцировать с помощью правила е) из § 3: k' (х) = F' (ω)*f (x). Вследствие формулы (2) и поскольку f' (х) = а, это выражение принимает вид:

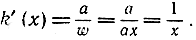
Итак, функция k (х) имеет ту же производную, что и функция F (х); а раз так, то согласно сказанному на стр. 473 мы имеем тождество

где с есть постоянная, не зависящая от значения переменной х. Константа с определяется с помощью простой подстановки х = 1 в последнее равенство. Из определения (1) следует, что

(так как интеграл, взятый в качестве определения, при значении х = 1 имеет равные верхний и нижний пределы). Теперь мы можем написать

т. е. с = ln а, а потому при любом х справедливо тождество

Полагая х = b, мы получим, наконец, искомую формулу (3). В частности, при а = х мы найдем последовательно, что

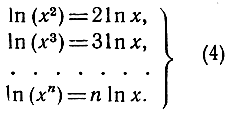
Из равенств (4) можно заключить, что при неограниченном возрастании х значения функции In x также возрастают неограниченно. Достаточно заметить, например, что

in(2") = /iln2,

причем правая часть, очевидно, неограниченно возрастает вместе с n, и вспомнить, что было установлено свойство монотонного возрастания функции ln х. Далее, мы имеем

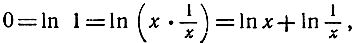
так что

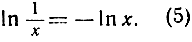
Наконец, справедливо равенство

при любом рациональном показателе 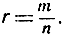В самом деле, полагая х^r = u, мы получаем

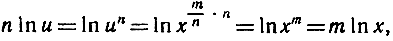
откуда следует

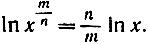
Поскольку In х есть монотонная и непрерывная функция от х, принимающая значение 0 при х = 1 и стремящаяся к бесконечности при неограниченном возрастании x, должно существовать некоторое число x, большее, чем единица, и такое, что для него будет иметь место равенство ln х = 1. Следуя Эйлеру, обозначим это число буквой е. (Тождественность этого определения с определением, данным на стр. 330, будет доказана позднее.) Итак, число е определено уравнением

Мы ввели число е, опираясь на свойство непрерывных функций, обеспечивающее существование корня этого уравнения. Теперь мы продолжим наше изыскание, чтобы как следствие получить явные формулы, позволяющие вычислить е с какой угодно точностью.