§ 6. Показательная (экспоненциальная) функция и логарифм

Концепции анализа предоставляют возможность построить гораздо более полную -теорию логарифма и показательной функции, чем это делает та элементарная процедура, которая лежит в основе обычного преподавания в школе. Там обычно отправляются от целых степеней аⁿ положительного числа а, а затем определяют корень 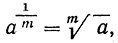получая, таким образом, значения а^r при любом рациональном показателе 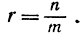Затем значение степени а^х при иррациональном х определяется так, что ах должна быть непрерывной функцией от x,- деликатный вопрос, обыкновенно опускаемый в элементарном изложении. Наконец, логарифмом числа у при основании а называется функция, обратная по отношению к показательной функции y = а^х.

В последующем изложении теории этих функций, построенном на основах анализа, ход мыслей противоположный. Мы начнем с логарифма, а затем придем к показательной функции.