3. Формула Лейбница для π

Последний результат приводит к одной из красивейших математических формул, открытых в XVII в.,- к знакопеременному ряду Лейбница, позволяющему вычислить π:

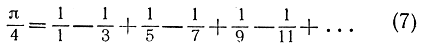
Символ +..., следует понимать в том смысле, что последовательность конечных "частных сумм", получающихся, когда в правой части равенств берется лишь n членов суммы, стремится к пределу при неограниченном возрастании n.

Чтобы доказать эту замечательную формулу, нам достаточно вспомнить формулу суммы конечной геометрической прогрессии

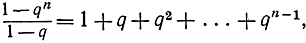
или

Если в последнее алгебраическое тождество подставим q = -x², то получим

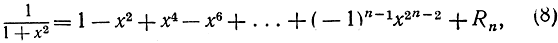
где "остаточный член" R_n выражается формулой

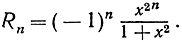
Равенство (8) можно проинтегрировать в пределах от 0 до 1. Следуя правилу а) из § 3, мы должны взять в правой части сумму интегралов от отдельных слагаемых. На основании (4) мы знаем, что

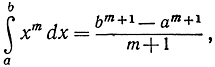
откуда, в частности, получим 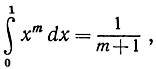а следовательно,

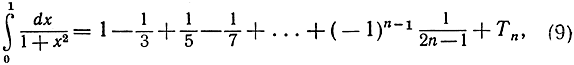
где 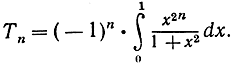Согласно формуле (5), левая часть формулы (9) равна . Разность между и частной суммой

равна 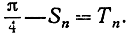Остается доказать, что Т_n стремится к нулю при возрастании n. Мы имеем неравенство

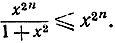
Вспомнив формулу (13) § 1, устанавливающую неравенство

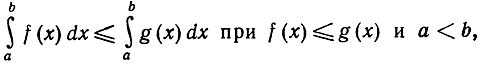
мы видим, что

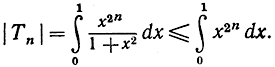
Правая часть в этом неравенстве согласно формуле (4) равна 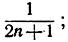поэтому 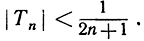Окончательно имеем неравенство:

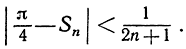
Так как 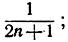стремится к нулю, то это и показывает, что S_n стремится к при возрастании n. Таким образом, формула Лейбница доказана.