2. Первые применения. Интегрирование функций x^r, cos x, sin х. Функция arctg х

Здесь невозможно дать исчерпывающее представление о роли основной теоремы, и мы ограничимся тем, что приведем несколько выразительных примеров. В задачах, встречающихся в механике и физике или в самой математике, очень часто приходится подсчитывать числовое значение некоторого определенного интеграла. Прямая попытка найти интеграл как предел может быть непреодолимо трудной. С другой же стороны, как мы это видели в § 3, любое дифференцирование выполняется сравнительно легко, и без труда возможно накопить очень большое количество формул дифференцирования. Каждая такая формула G' (х) = f (x), обратно, может быть рассматриваема как формула, определяющая первообразную функцию G (х) от функции f (х).

Формула (3) позволяет использовать известную первообразную функцию для вычисления интеграла от функции f (х) в некотором данном промежутке.

Если мы, например, хотим найти интегралы от степеней x², х³ или в общем виде хⁿ, то самое простое - это действовать, как указано в § 1. По формуле дифференцирования степени производная от хⁿ равна nx^n-1, так что производная от функции

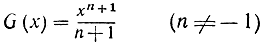
есть функция

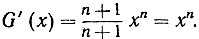
В таком случае функция 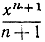является первообразной функцией по отношению к функции f (х) = х, а следовательно, мы немедленно получаем формулу

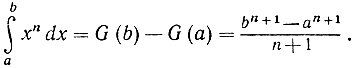
Это рассуждение несравненно проще громоздкой процедуры непосредственного вычисления интеграла как предела суммы.

Как более общий случай, мы нашли в § 3, что при любом рациональном s, как положительном, так и отрицательном, производная функции х равна sx^s-1, а потому при s = r + 1 функция

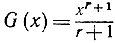
имеет производную f (х) = G' (х) = х^r (мы предполагаем, что r≠- 1, т. е. что s≠0). Итак, функция 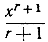есть первообразная функция, или "неопределенный интеграл" от х^r, и мы получаем (при положительных а и b и при r≠- 1) формулу

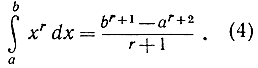
В формуле (4) приходится предполагать, что стоящая под интегралом функция х^r определена и непрерывна в промежутке интегрирования, так что нужно исключить точку х = 0, если r<0. Вот потому мы и вынуждены допустить, что в этом случае а и b положительны.

Если положим G (х) = - cos х, то получим G' (х) = sin x, и отсюда возникает соотношение

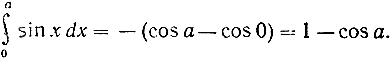
Аналогично если G (x) = sin x, то G' (x) = cos x, и, значит,

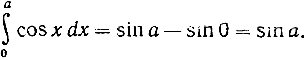
Особенно интересный результат получается из формулы дифференцирования функции arctg x:

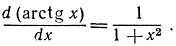
Раз функция arctg x есть первообразная по отношению к функции 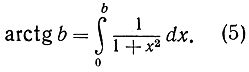то на основании формулы (3) можно написать:

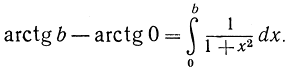
Но arctg 0 = 0 (нулевому зиачению тангенса соответствует нулевое значение угла). Итак, мы имеем:

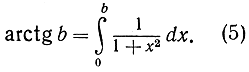
в пределах от 0 до 1 равна ">
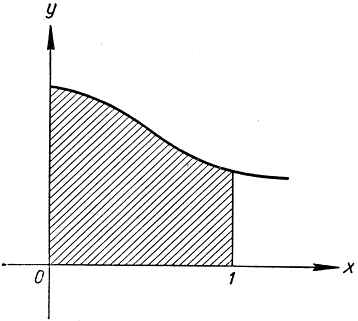
Рис. 276. Площадь под кривой 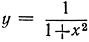в пределах от 0 до 1 равна

В частности, если b = 1, то arctg b равно (значению тангенса, равному

1, соответствует угол в 45°, что в радианной мере составляет ). Таким образом, мы получаем замечательную формулу

Это показывает, что площадь под графиком функции y = 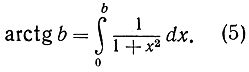в пределах от х = 0 до х = 1 равна четверти площади единичного круга.