§ 5. Основная теорема анализа

1. Основная теорема

Понятие об интегрировании, и в некоторой мере о дифференцировании, было хорошо развито раньше работ Ньютона и Лейбница. Но было совершенно необходимо сделать одно очень простое открытие, для того чтобы дать толчок к огромной эволюции вновь созданного математического анализа. Два как будто бы взаимно не соприкасающихся предельных процесса, употребляемые ©дин для дифференцирования, другой для интегрирования функций, оказались тесно связанными между собой. В самом деле, они являются взаимно обратными операциями, подобно таким операциям, как сложение и вычитание, умножение и деление. Дифференциальное и интегральное исчисления представляют собой нечто единое.

Великое достижение Ньютона и Лейбница заключается в том, что они впервые ясно осознали и использовали эту основную теорему анализа. Без сомнения, их открытие лежало на прямом пути естественного научного развития, и нисколько не удивительно, что различные лица пришли независимо и почти одновременно к ясному пониманию указанного выше обстоятельства.

Для того чтобы точно сформулировать основную теорему, рассмотрим интеграл от функции y = f (х) в пределах от постоянного числа а до числа х, которое будем считать переменным. Чтобы не смешивать верхнего предела интегрирования х с переменной, фигурирующей под знаком интеграла, запишем интеграл в следующем виде (см. стр. 435):

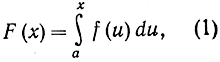
демонстрируя таким образом наше намерение изучать интеграл как функцию F (х) своего верхнего предела (рис. 274). Эта функция F (х) есть площадь под кривой y = f (u) от точки u = а до точки u = х. Иногда интеграл F (х) с переменным верхним пределом называют "неопределенным интегралом".

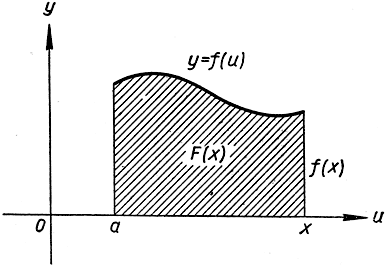
Рис. 274. Интеграл как функция верхнего предела

Основная теорема анализа читается следующим образом: Производная неопределенного интеграла (1) по его верхнему пределу х равна значению функции f (u) в точке u = х:

Другими словами, процесс интегрирования, ведущий от функции f(x) к функции F (x), "уничтожается" обратным ему процессом дифференцирования, применяемым к функции F (х).

На интуитивной основе доказательство этого предложения не представляет труда. Оно базируется на интерпретации интеграла F (х) как площади, и было бы затемнено, если бы мы попытались представлять функцию F (х) в виде графика и истолковывать производную F' (х) как соответствующий наклон. Оставляя в стороне установленную ранее геометрическую интерпретацию производной, мы сохраним геометрическое толкование интеграла F (х) как площади, а дифференцировать функцию F (х) станем аналитическим методом. Разность

есть просто площадь под кривой y = f (u) между пределами u = х₁ и u = х (рис. 275), и нетрудно понять что числовое значение этой площади заключено между числами (х₁ - х)m и (x₁ - х) М:

где М и m являются соответственно наибольшим и наименьшим значениями функции f (u) в промежутке от u = х до u = x₁. Действительно, эти произведения дают площади двух прямоугольников, из которых один содержит рассматриваемую криволинейную область, а другой содержится в ней.

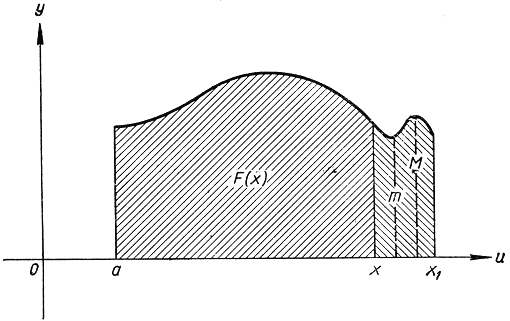
Рис. 275. К доказательству основной теоремы

Отсюда следует:

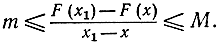
Предположим, что функция f (u) непрерывна, так что при стремлении x₁ к х обе величины М и m стремятся к значению функции f (u) в точке u = х, т. е. к значению f (х). В таком случае можно считать доказанным, что

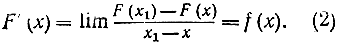
Интуитивный смысл этого результата заключается в том, что при возрастании скорость изменения площади под кривой y = f (х) равна высоте кривой в точке х.

В некоторых руководствах содержание этой основной теоремы затемняется неудачно выбранной терминологией. Именно, многие авторы сначала вводят понятие производной, а затем определяют "неопределенный интеграл" просто как результат операции, обратной по отношению к дифференцированию: они говорят, что функция G (х) есть неопределенный интеграл от функции f (х), если

Таким образом, этот способ изложения непосредственно связывает дифференцирование со словом "интеграл". Только позднее вводится понятие "определенный интеграл", трактуемое как площадь или как предел последовательности сумм, причем недостаточно подчеркивается, что слово "интеграл" обозначает теперь нечто совершенно другое, чем прежде. И вот оказывается, что самое главное, что содержится в теории, приобретается лишь украдкой с черного хода, и учащийся встречается с серьезными затруднениями в своих усилиях понять существо дела. Мы предпочитаем функции G (х), для которых G' (х) = f (х), называть не "неопределенными интегралами", а первообразными функциями от функции f (х). Тогда основная теорема может быть сформулирована следующим образом:

Функция F (х), являющаяся интегралом от функции f (x) при постоянном нижнем и переменном верхнем пределе х, есть одна из первообразных функций от функции f (x).

Мы говорим "одна из" первообразных функций по той причине, что если G (х) является первообразной функцией от f (х), то непосредственно ясно, что и любая функция вида Н (х) = G (х) + с (с - произвольная постоянная) есть также первообразная, так как Н' (х) = G' (х). Обратное утверждение также справедливо. Две первообразные функции G (х) и Н (х) могут отличаться одна от другой не иначе, как постоянным слагаемым. Действительно, разность U (х) = G (х) - Н (х) имеет в качестве производной U' (х) = G' (х) - Н' (х) = f (х) - f (х) = 0, т. е. эта разность постоянна, так как очевидно, что если график функции в каждой своей точке горизонтален, то сама функция, представляемая графиком, непременно должна, быть постоянной.

Это ведет к очень важному правилу вычисления интеграла в пределах от а до b - в предположении, что нам известна какая-либо первообразная функция G (х) от функции f (x). Согласно нашей основной теореме функция

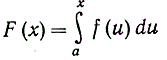
есть также первообразная функция от функции f (х). Значит, F (х) = G (х) + с, где с - постоянная. Значение этой постоянной определится, если мы примем во внимание, что 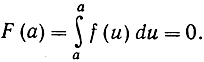Отсюда следует: 0 = G (а) + с, так что с = - G (а). Тогда определенный интеграл в пределах от а до х тождественно удовлетворяет равенству

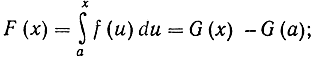
замена х через b приводит к формуле

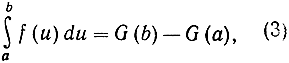
независимо от того, какая именно из первообразных функций была "пушена в ход". Другими словами, чтобы вычислить определенный интеграл 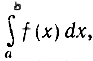достаточно найти такую функцию G (х), для которой G' (х) = f (x), и затем составить разность G (b) - G (а).