§ 4. Обозначения Лейбница и "бесконечно малые"

Ньютон и Лейбниц умели находить интегралы и производные как пределы. Но самые основания анализа были долго окружены таинственностью вследствие нежелания признать за понятием предела исключительного права быть источником новых методов. Ни Ньютон, ни Лейбниц не смогли занять ту отчетливую позицию, которая нам кажется простой и естественной теперь, когда понятие предела полностью выяснено. Их пример господствовал больше столетия, в течение которого сущность дела была затемнена бесплодными рассуждениями о "бесконечно малых величинах", о "дифференциалах", о "последнем отношении" и т. д. Неохота, с которой эти понятия были, в конце концов, отвергнуты, глубоко коренилась в философских концепциях того времени и в самой природе человеческого мышления. Казалось, что можно рассуждать так: конечно, интеграл и производную можно вычислить как пределы. Но все же, в конце концов, чем же являются эти объекты "в себе", независимо от того специфического способа их описания, каким является предельный переход. Ведь интуитивные понятия - такие, как площадь или наклон кривой,- имеют как будто бы абсолютный смысл "в себе", и нет надобности в привлечении каких-либо вспомогательных вписанных многоугольников или секущих и их пределов. Без сомнения, желание сформулировать адекватные определения площади или наклона кривой как "вещей в себе" вполне оправдано с психологической точки зрения. Но при зрелых установках, которые так часто расчищали путь к подлинному прогрессу мысли, приходится отбросить это желание и в предельном переходе видеть их единственное приемлемое в научном смысле определение. В XVII в. не было интеллектуальных традиций, которые допускали бы такой радикализм.

Попытка Лейбница "объяснить" производную стоит в непосредственной и безупречной связи с введенным им обозначением для разностного отношения функции f (х)

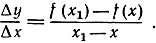
Предел этого отношения, т. е. производную (которую мы, следуя обычаю, введенному впоследствии Лагранжем, обозначили через f' (х)), Лейбниц записывает с помощью символа

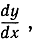
заменяя, таким образом, символ разности "дифференциальным символом" d. Никаких трудностей и никакой таинственности не возникает при условии ясного понимания того, что этот символ является всего лишь указанием на необходимость осуществить предельный переход при Δх → 0, что влечет за собой Δy → 0. До перехода к пределу в разностном отношении 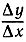нужно сократить числитель и знаменатель на Δх или суметь преобразовать это отношение так, чтобы переход к пределу совершался безболезненно. Это и является в каждом отдельном случае узловым пунктом процесса дифференцирования. Если бы попробовали перейти к пределу без таких предварительных сокращений, то получили бы не имеющее смысла выражение 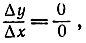что не принесло бы нам никакой пользы. Таинственность и неясность наступают только в том случае, если мы, по примеру Лейбница или многих его последователей, стали бы говорить нечто подобное следующему: "Δх не стремится к нулю. Напротив, "последнее значение" Δх не есть нуль, а является "бесконечно малой величиной", "дифференциалом", обозначаемым символом dx; аналогично Δy имеет "последнее" бесконечно малое значение dy. Настоящее отношение этих бесконечно малых дифференциалов есть опять обыкновенное число 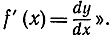Поэтому Лейбниц и называл производную "дифференциальным отношением". Такие бесконечно малые величины рассматривались как некие новые числа, хотя и отличные от нуля, но меньшие любого положительного числа из системы действительных чисел.

Считалось, что такие понятия доступны лишь немногим избранным, обладающим настоящим математическим чутьем, и что анализ поэтому, по существу, очень труден, так как не всякий обладает этим чутьем или может его развить. Интеграл аналогичным образом рассматривался как сумма "бесконечно большого числа бесконечно малых слагаемых", а именно вида f(x) dx. Существовало представление, будто такая сумма есть интеграл или площадь, в то время как вычисление ее значения как предела последовательности конечных сумм обыкновенных слагаемых f (x_j) Δx, рассматривалось как некий придаток. Теперь мы попросту отбрасываем желание "непосредственного" объяснения и определяем интеграл как предел последовательности конечных сумм. Этим путем все трудности устраняются, и все, что ценно в анализе, приобретает твердую основу.

Несмотря на все сказанное выше, в дальнейшем употребление обозначений Лейбница: 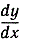для производной и 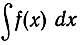для интеграла - не только сохранилось, но и оказалось чрезвычайно полезным. Против такого употребления нечего возразить, если не упускается из виду, что символ d есть только символ перехода к пределу. Преимущество обозначений Лейбница состоит в том, что с пределами отношений или сумм можно в какой-то мере оперировать так, "как если бы" они были в самом деле отношениями или суммами. Подсказывающая сила этой символики всегда вводила в соблазн приписывать этим символам некоторый совершенно нематематический смысл. Если не поддаваться этому соблазну, то обозначения Лейбница являются по меньшей мере превосходным сокращением более громоздких явных выражений, содержащих предельный переход; по существу же они совершенно необходимы в более развитых частях теории.

Например, правило d) (стр. 463-464) дифференцирования функции x = g (y), обратной по отношению к функции y = f (x), заключалось в равенстве g'(y) f'(x) = 1. В обозначениях Лейбница оно выглядит следующим образом: 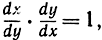т. е. так, "как если бы" можно было сокращать на дифференциалы подобно тому, как это делается с обыкновенными дробями. Аналогично запись в дифференциальной форме выведенного на стр. 465 правила е) дифференцирования сложной функции z = k (x), где

имеет вид:

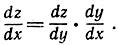
Кроме того, обозначения Лейбница обладают еще и тем преимуществом, что они указывают явно на сами величины х, y, z в большей степени, чем на их функциональные взаимоотношения. Последние выражают некоторую процедуру, т. е. совокупность операций, с помощью которых из одной величины x получается другая y; например, функция y = f(x) = x² определяет величину y, равную квадрату величины х. Именно сама операция, в данном случае возвышение в квадрат, есть предмет внимания математики. Физики же или инженеры в первую очередь интересуются самими величинами. Поэтому акцентирование самих величин в обозначениях Лейбница имеет особенную привлекательность для лиц, занимающихся прикладной математикой.

Присоединим еще одно замечание. В то время как "дифференциалы" в качестве бесконечно малых величин из математического обихода изгнаны теперь окончательно, и не без позора, само слово "дифференциал" прокралось обратно через заднюю дверь, правда на этот раз для того, чтобы обозначить безукоризненно законное и полезное понятие. Теперь оно обозначает просто разность ΔΔΔх, когда Δх мало по сравнению с другими рассматриваемыми величинами. Но здесь мы не можем вступать в обсуждение роли, которую это понятие играет в приближенных вычислениях. Не будем мы также рассматривать другие математические объекты, законно именуемые "дифференциалами" и в некоторых случаях показавшие себя весьма полезными в анализе и его приложениях к геометрии.