§ 3. Техника дифференцирования

До сих пор наши усилия были направлены на то, чтобы продифференцировать целый ряд отдельных функций, причем мы предварительно придавали надлежащий вид разностному отношению. Важным шагом вперед в работах Ньютона, Лейбница и их последователей была замена этих разрозненных индивидуальных приемов мощными общими методами. С помощью этих методов можно почти автоматически дифференцировать любую функцию из числа тех, с которыми обыкновенно приходится иметь дело в математике; нужно только запастись небольшим числом простых правил и уметь их применять. Совокупность этих приемов приобрела характер вычислительного "алгорифма".

Мы не можем вникать в подробности этой техники. Укажем только немногие наиболее простые правила.

а) Дифференцирование суммы. Если а и b - постоянные и функция k (x) задана формулой

то, как это легко докажет сам читатель, справедливо следующее:

Аналогичное правило имеет место при любом числе слагаемых.

b) Дифференцирование произведения. Производная произведения

выражается формулой

Это легко доказывается следующим приемом: прибавим и отнимем от р (х + h) - р (х) одно и то же выражение, а именно f (х + h) g (x):

Объединяя первые два и последние два члена, мы получим:

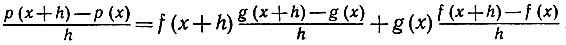
Заставим теперь h стремиться к нулю; поскольку f (х + h) при этом стремится к f (х), наше утверждение доказывается немедленно.

Упражнение. Пользуясь этим правилом, доказать, что производная функции р (х)= хⁿ есть р' (x) = nx^n-1. (Указание. Примите во внимание, что хⁿ = x*x^n-1, и примените математическую индукцию.)

С помощью правил а) и b) можно дифференцировать любой полином

его производная равна выражению

В качестве одного из применений можно доказать биномиальную теорему (см. стр. 40). Согласно этой теореме степень бинома (1 + х)ⁿ разлагается в полином следующего вида:

где коэффициент a_k дается формулой

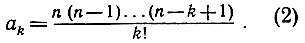
Мы уже видели (упражнение на стр. 454), что дифференцирование левой части формулы (1) дает n (1 + х)^n-1. На основании предыдущего пункта

Если теперь в этой формуле положить х = 0, то получим n = a₁, что соответствует формуле (2) при k = 1. Снова продифференцируем формулу (3) и тогда будем иметь:

Подстановка в эту формулу нуля вместо х дает n (n - 1) = 2а₂ в соответствии с формулой (2) при k = 2.

Упражнение. Доказать формулу (2) при k = 3 и при любом k (с помощью математической индукции).

c) Дифференцирование частного. Если

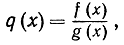
то

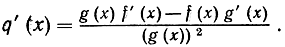
Доказательство представляется в виде упражнения читателю. Очевидно, нужно предполагать, что g (х) ≠ 0.

Упражнение. С помощью последнего правила вывести производные от tg x и ctg х, зная производные от sin х и cos х. Доказать, что производными от 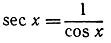и 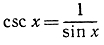являются соответственно 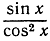и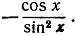

Мы умеем теперь дифференцировать любую функцию, являющуюся отношением двух многочленов. Например,

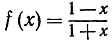
имеет производную

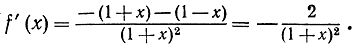
Упражнение. Продифференцировать функцию

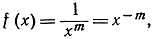
предполагая m целым положительным. Результат:

d) Дифференцирование обратных функций. Если функции

взаимно обратны (например, y = х² и x = √y), то производная одной из них является обратной величиной по отношению к производной другой.

Именно,

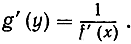
Это утверждение легко доказать, если обратиться к взаимно обратным разностным отношениям 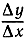и 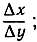это видно ясно также из геометрической интерпретации обратных функций, приведенной на стр. 311, если отнести наклон касательной к оси y, а не к оси х.

В качестве примера продифференцируем функцию

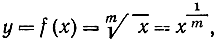
обратную по отношению к функции x = y^m (см. также более полное рассуждение, относящееся к случаю m = ¹/₂, на стр. 454). Поскольку функция х = y^m имеет своей производной выражение my ^m-1, то мы имеем

откуда, делая подстановки 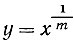и y^-m = x^-1, получим:

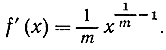
В качестве следующего примера продифференцируем обратную тригонометрическую функцию (см. стр. 312)

Для того чтобы обеспечить однозначное определение функции y, предположим, что переменная y, обозначающая меру угла в радианах, ограничена промежутком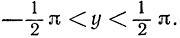

Мы знаем (см. стр. 456), что 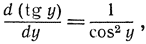и так как

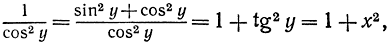
то можно заключить, что

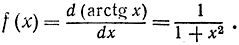
Таким же точно путем читатель сможет вывести следующие формулы:

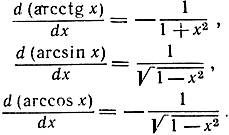
Наконец, мы приходим к следующему важному правилу:

е) Дифференцирование сложных функций. Сложные функции составляются из двух (или нескольких) простых (см. стр. 313). Например, функция z = sin √x составлена из функций z = sin y и y = √x; функция z = √x + √x⁵ составлена из функций z = y + y⁵ и y = √х; функция z = sin (x²) - из функций z = sin y и y = х²; функция 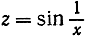- из функции z = sin y и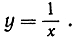

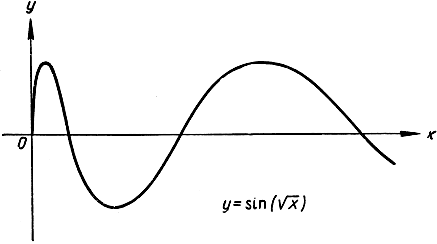
Рис. 272. y = sin (√x)

Если из двух данных функций

вторую подставить в первую, то получается сложная функция

Докажем справедливость формулы

С этой целью составим разностное отношение

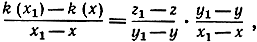
где y₁ = f (x₁) и z₁ = g (y₁) = k (x₁); при стремлении х₁ к х левая часть стремится к k' (х), а два множителя в правой части стремятся соответственно к g'(y) и к f'(x), чем и доказывается формула (4).

В этом доказательстве было необходимо условие y₁ - y ≠ 0. В самом деле, мы делили на Δy = y₁ - y; поэтому нужно было считать исключенными те значения х₁, при которых y₁ - y = 0. Однако формула (4) остается в силе даже в том случае, если Ау равно нулю в промежутке, окружающем точку х. При этом предположении у остается постоянным, так что f' (х) = 0; с другой стороны, и k (х) = g (y) остается постоянным относительно x (поскольку y не меняется при изменении х) и, следовательно, k' (x) = 0; итак, формула (4) справедлива также и в рассматриваемом случае.

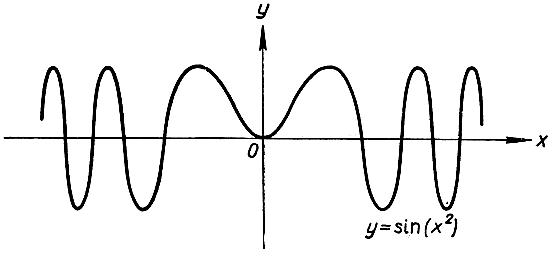
Рис. 273. y = sin (x² )

Читатель должен проверить следующие примеры:

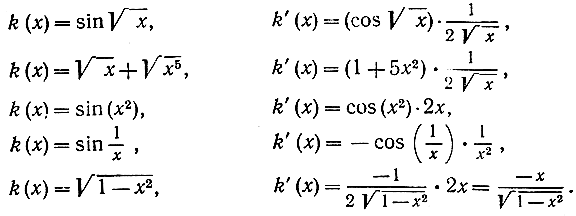
Упражнение. Сопоставляя результаты стр. 454 и стр. 465, доказать, что функция

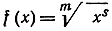
имеет производную

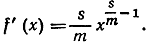
Теперь можно уже отметить, что все наши формулы, касающиеся степеней x, могут быть объединены в одну общую:

При любом положительном или отрицательном рациональном r функция

имеет производную

Упражнения.

1. Произвести дифференцирования в упражнениях на стр. 455, пользуясь только что выведенными правилами.
2. Продифференцировать следующие функции:
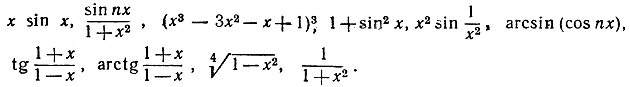
3. Найти вторые производные от некоторых из вышеприведенных функций и от следующих функций:
   
   
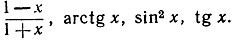
4. Продифференцировать функцию
   
   
   и доказать минимальные свойства отраженного и преломленного луча, установленные в главе VII (стр. 363 и стр. 414). Предполагается, что отражение и преломление происходят в точке на оси х и что данные начальная и конечная точки заданы координатами (х₁, y₁) и (х₂, y₂). (Примечание. Производная от этой функции обращается в нуль только в одной точке, и, поскольку в этой точке неизбежно имеется минимум, а не максимум, нет необходимости исследовать вторую производную.) Дальнейшие задачи на максимум и минимум.
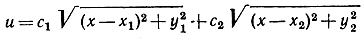
5. Найти экстремумы следующих функций, наметить их графики, определить промежутки возрастания, убывания, выпуклости и вогнутости:
   
   
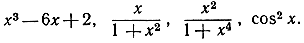
6. Изучить максимумы и минимумы функции x³ + 3ax + 1 в зависимости от значения параметра а.
7. Какая из точек гиперболы 2y² - х² = 2 - самая близкая к точке х = 0, y = 3?
8. Из всех прямоугольников данной площади найти прямоугольник с самой короткой диагональю.
9. Вписать прямоугольник наибольшей площади в эллипс
   
   
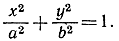
10. Из всех круговых цилиндров данного объема найти цилиндр с наименьшей поверхностью.