8. Максимумы и минимумы

Чтобы найти наибольшие и наименьшие значения заданной функции f (х), мы прежде всего должны составить ее производную f' (х), найти затем те значения х, при которых эта производная обращается в нуль, и, наконец, исследовать, в каких точках из числа найденных функция имеет максимум и в каких - минимум. Последний из этих вопросов может быть решен с помощью второй производной f" (x), знак которой указывает на выпуклость или вогнутость графика кривой; если же вторая производная обращается в нуль, то обыкновенно это указывает на то, что мы имеем дело с точкой перегиба, и тогда экстремума нет.

Принимая во внимание знаки первой и второй производных, можно не только найти экстремумы функции, но и определить вид ее графика. Указанный способ позволяет нам выделить те значения х, при которых функция имеет экстремум; для того чтобы найти соответствующие значения самой функции y = f (х), нужно сделать подстановку найденных значений х в выражение f (x).

В качестве примера рассмотрим многочлен:

его производные выражаются формулами:

Квадратное уравнение f (х) = 0 имеет корни х₁ = 1, х₂ = 2, и в этих точках значения второй производной равны f" (х₁) = -6<0, f" (x₂) = 6>0.

Следовательно, функция f (х) имеет максимум f (х₁) = 6 и минимум _{f (x2) = 5}.

Упражнения.

1. Наметить график рассмотренной функции.
2. Исследовать и наметить график функции f (x) = (х² - 1) (x² - 4).
3. Найти минимум функций 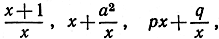считая значения р и q положительными. Имеют ли максимум эти функции?
4. Найти максимум и минимум функций sin x и sin (x²).