4. Закон движения Ньютона

Хотя более подробный анализ подобных явлений нами не предусмотрен, мы все же хотим включить их в общую схему, на основе которой Ньютон произвел подлинную революцию в механике и физике.

Рассмотрим вместе с Ньютоном движение некоторой частицы, имеющей массу m; обозначим ее пространственные координаты, являющиеся функциями времени t, через х(t),y(t), z(t); таким образом, компоненты ускорения равны вторым производным x"(t), y"(t), z"(t). В истории науки фактом решающего значения оказалось осознание Ньютоном того, что величины mх", my", mz" могут быть рассматриваемы как компоненты силы, действующей на частицу. С первого взгляда может показаться, что в этой формулировке содержится всего лишь формальное определение понятия "силы". Но большой успех Ньютона заключается в том, что он первый привел это определение в соответствие с действительными явлениями природы: дело обстоит так, как будто бы сама природа предоставляла силовое "поле", которое мы можем считать известным, тогда как нам ничего неизвестно заранее об интересующем нас движении частицы в этом поле. Величайший триумф ньютоновской динамики - обоснование законов Кеплера о движении планет - ясно показывает полную гармонию между математическими концепциями Ньютона и явлениями природы. Прежде всего Ньютон предположил, что сила тяготения обратно пропорциональна квадрату расстояния. Если мы допустим, что Солнце находится в начале координатной системы, и примем величины х, y, z за координаты данной планеты, то компоненты силы по направлениям трех координатных осей будут равны соответственно

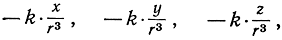
где k есть постоянная тяготения, не зависящая от времени, а 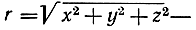расстояние от Солнца до планеты. Эти выражения определяют силовое поле независимо от движения в нем частицы. Известные нам данные, характеризующие это поле, нужно связать с общим ньютоновым законом движения (т. е. связать кинематические и динамические элементы); приравнивая два различных выражения вектора, мы получим систему трех дифференциальных уравнений

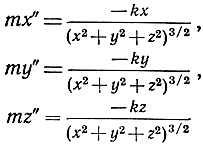
с тремя неизвестными функциями x(t), y(t), z(t). Эту систему можно решить, и тогда обнаружится, что в полном согласии с кеплеровскими эмпирическими наблюдениями орбита планеты есть коническое сечение с Солнцем в одном из фокусов, что площади, описываемые в равные промежутки времени радиусом-вектором, проведенным от Солнца к планете, равны между собой и что квадраты периодов полного обращения двух планет вокруг Солнца пропорциональны кубам их расстояний от Солнца. Доказательство этих утверждений мы вынуждены опустить.

Задача о колебательном движении предоставляет более элементарную иллюстрацию метода Ньютона. Предположим, что мы имеем частицу, движущуюся по прямой линии, по оси х, и связанную с началом координат силой упругости, что можно, например, осуществить с помощью пружины или резинки.

Если частица выведена из положения равновесия (в начале координат) и помещена в некоторую точку с координатой х, то сила потянет ее назад. Мы предположим, что эта сила пропорциональна растяжению х; так как она направлена к началу координат, то представится в виде - k²x, где -k² - отрицательный множитель пропорциональности, выражающий силу упругости пружины или резинки.

Мы предположим, далее, что налицо имеется трение, замедляющее движение, и что это трение пропорционально скорости х' частицы с коэффициентом пропорциональности, равным - r. Тогда результирующая сила в любой момент времени выразится через -k²x - rх', и, пользуясь общим принципом Ньютона, мы приходим к уравнению mх" = -k²x - rx' или

А это - не что иное, как рассмотренное выше дифференциальное уравнение (И) затухающих колебаний. Предыдущий простой пример имеет большое значение, так как многие колебания механических или электрических систем могут быть математически записаны с помощью именно этого дифференциального уравнения. Здесь мы имеем типичный пример того, как отвлеченная математическая формулировка одним ударом обнажает внутреннюю структуру многих, казалось бы, совершенно различных и не связанных между собой отдельных явлений. Подобного рода абстрагирование от частного характера данного явления и переход к общему закону, регулирующему обширный класс явлений, есть характерная черта математической трактовки физических проблем.