6. Производная и скорость. Вторая производная и ускорение

До сих пор понятие производной мы связывали с геометрическим представлением графика функции. Однако было бы грубой ошибкой ограничивать роль понятия производной одной лишь задачей об определении наклона касательной к данной кривой. Еще более важной с научной точки зрения задачей является вычисление скорости изменения какой бы то ни было величины f (t), меняющейся с течением времени t. Именно с этой стороны Ньютон и подошел к дифференциальному исчислению. В частности, Ньютон стремился проанализировать явление скорости, рассматривая время и положение движущейся частицы как переменные величины (по выражению Ньютона, "флюэнты"). Когда некоторая частица движется вдоль оси х, то ее движение вполне определено, раз задана функция х = f (t), указывающая положение частицы х в любой момент времени t. "Равномерное движение" с постоянной скоростью b по оси х определяется линейной функцией х = а + bt, где а есть положение частицы в начальный момент (при t = 0).

Движение частицы на плоскости описывается уже двумя функциями

которые определяют ее координаты как функции времени. В частности* равномерному движению соответствуют две линейные функции

где b и d - две "компоненты" постоянной скорости, а a и с - координаты начального положения частицы (при t = 0); траекторией частицы является прямая линия, уравнение которой

получается путем исключения t из двух стоящих выше соотношений.

Если частица движется в вертикальной плоскости х, у под действием одной лишь силы тяжести, то движение ее (это доказывается в элементарной физике) определено двумя уравнениями

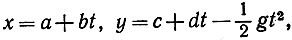
где а, b, с, d - постоянные величины, зависящие от состояния частицы в начальный момент, а g - ускорение силы тяжести, равное приблизительно 9,81, если время измеряется в секундах, а расстояние - в метрах. Траектория движения, получаемая путем исключения t из двух данных уравнений, есть парабола

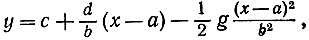
если только b≠0; в противном случае траекторией является отрезок вертикальной оси.

Если частица вынуждена двигаться по некоторой данной кривой (подобно тому как поезд движется по рельсам), то движение ее может быть определено функцией s (t) (функцией времени t), равной длине дуги s, вычисляемой вдоль данной кривой от некоторой начальной точки Р₀ до положения частицы в точке Р в момент времени t. Например, если речь идет о единичном круге х² + y² = 1, то функция s = ct определяет на этом круге равномерное вращательное движение со скоростью с.

^*Упражнение. Начертить траектории плоских движений, заданных уравнениями: 1) х = sin t, y = cos t; 2) х = sin 2t, y = cos 3t; 3) х = sin 2t, y = 2 sin 3t; 4) в описанном выше параболическом движении предположить начальное положение частицы (при t = 0) в начале координат и считать b>0, d>0. Найти координаты самой высокой точки траектории. Найти время t и значение х, соответствующие вторичному пересечению траектории с осью х.

Первой целью, которую поставил себе Ньютон, было нахождение скорости частицы, движущейся неравномерно. Рассмотрим для простоты движение частицы вдоль некоторой прямой линии, заданное функцией х = f (t). Если бы движение было равномерным, т. е. совершалось с постоянной скоростью, то эту скорость можно было бы найти, взяв два момента времени t и t₁ и соответствующие им положения частиц f (t) и f (t₁) и составив отношение

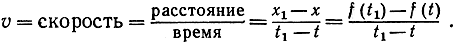
Например, если t измерено в часах, а х в километрах, то при t₁ - t = 1 разность х₁ - х будет числом километров, пройденных за 1 час, а v - скоростью (в километрах в час). Говоря, что скорость есть величина постоянная, имеют в виду лишь то, что разностное отношение

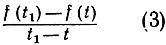
не изменяется при любых значениях t и t₁. Но если движение неравномерно (что имеет, например, место при свободном падении тела, скорость которого по мере падения возрастает), то отношение (3) не дает значения скорости в момент t, а представляет собой то, что принято называть средней скоростью в промежутке времени от t до t₁. Чтобы получить скорость в момент t, нужно вычислить предел средней скорости при стремлении t₁ к t. Таким образом, следуя Ньютону, мы определим скорость так:

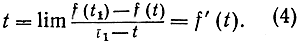
Другими словами, скорость есть производная от пройденного пути (координаты частицы на прямой) по времени, или "мгновенная скорость изменения" пути по отношению к времени - в противоположность средней скорости изменения, определяемой по формуле (3).

Скорость изменения самой скорости называется ускорением. Ускорение - это просто производная от производной; оно обычно обозначается символом f"(t) и называется второй производной от функции f (t).

Галилей заметил, что вертикальное расстояние х, проходимое при свободном падении тела в течение времени t, выражается формулой

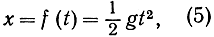
где g есть ускорение силы тяжести. Из формулы (5), путем дифференцирования ее, можно получить скорость v тела в момент времени t; эта скорость выражается формулой

а ускорение а, которое постоянно,- формулой

Предположим, что нужно найти скорость тела через 2 секунды после начала падения. Найдем сначала среднюю скорость за промежуток времени от t = 2 до t = 2,1:

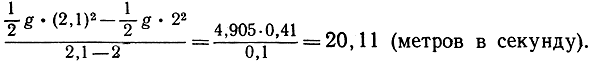
Подставляя же в формулу (6) значение t = 2, мы найдем, что значение мгновенной скорости в конце второй секунды равно 19,62 (метров в секунду).

Упражнение. Какова средняя скорость тела за промежуток времени от t = 2 до t = 2,01, от t = 2 до t = 2,001?

При движении точки на плоскости две производные f'(t) и g'(t) двух функций х = f (t) и y = g(t) определяют компоненты скорости. При движении вдоль заданной кривой скорость нужно определить как производную от функции s = f(t), где s - длина дуги.