
4. Производные от тригонометрических функций
Теперь мы приступим к чрезвычайно важному вопросу - к дифференцированию тригонометрических функций. Предварительно условимся, что измерение углов будем производить исключительно в радианах.
Чтобы продифференцировать функцию y = f (х) = sin x, положим х1 - х = h, так что х1 = х + h и f (х1) = sin х1 = sin (x + h). Воспользовавшись тригонометрической формулой для синуса суммы двух углов sin (A + В), мы получим:
f (х1) = sin (x + h) = sin x cos h + cos x sin h.
Отсюда
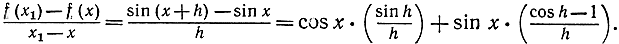
Если х1 стремится к х, то h стремится к 0, sin h стремится к 0, a cos h стремится к 1.
Применяя, далее, результаты стр. 340, мы получим:
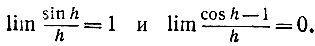
Правая часть соотношения (2) стремится, следовательно, к cos х, и мы получаем окончательный результат: функция f (x) = sin x имеет своей производной функцию f' (х) = cos x, или, короче,
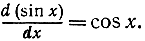
Упражнение. Доказать, что 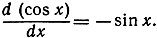
Чтобы продифференцировать функцию f (х) = tg x, мы напишем 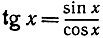 и получим, далее:
и получим, далее:
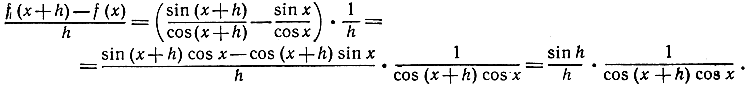
(Последнее равенство получается с помощью формулы sin (А - В) = sin A cos В - cos A sin В, где А = х + h, В = х.) Если h стремится к 0, то 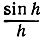 стремится к 1, cos (x + h) стремится к cos х, и отсюда мы делаем заключение:
стремится к 1, cos (x + h) стремится к cos х, и отсюда мы делаем заключение:
Производная функции f (х) = tg х есть функция 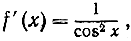 или
или
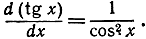
Упражнение. Доказать, что 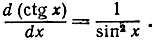
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'