3. Примеры

Может показаться, что рассуждения, приведшие к определению (1), лишены всякого практического смысла. В самом деле, одна проблема подменена другой: вместо того чтобы искать наклон касательной к кривой y = f (х) в некоторой точке, мы должны вычислять предел (1), что с первого взгляда кажется одинаково трудным. Но, как только мы откажемся от рассмотрений в общем виде и перейдем к отдельным функциям, мы получим весьма реальные результаты.

Простейшей из функций является функция f (х) = с, где с постоянно. График этой функции y = f (x) = с есть горизонтальная прямая, совпадающая со всеми своими касательными; очевидно, для всех значений х имеет место соотношение

Это вытекает также и из определения (1); в самом деле,

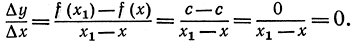
Таким образом, получаем тривиальный результат:

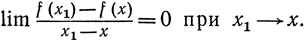
Вслед за этим рассмотрим простую функцию y = f (х) = х, графиком которой является биссектриса угла первого квадранта. Геометрически ясно, что для всех значений х

а аналитическое определение (1) снова дает

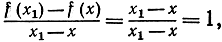
так что

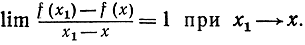
Простейшим нетривиальным примером является дифференцирование функции

что в сущности является нахождением наклона параболы. Это - простейший случай, на котором мы можем учиться совершать переход к пределу, когда результат с первого взгляда не очевиден. Мы имеем:

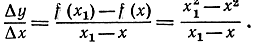
Если бы мы попытались перейти к пределу непосредственно в числителе и в знаменателе, то получили бы не имеющее смысла выражение ⁰/₀. Но этого затруднения можно избежать, сократив дробь на мешающий нам множитель х₁ - х до перехода к пределу. (Такое сокращение законно, так как при вычислении предела разностного отношения мы считаем, что х₁≠x см. стр. 337.) Таким образом мы получаем результат:

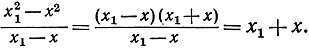
После сокращения нахождение предела при х₁→х не представляет уже никаких трудностей. Этот предел получается путем простой "подстановки", так как разностное отношение в своем новом виде х₁ + х непрерывно, а предел непрерывной функции при х₁ → х есть просто значение этой функции при х₁ = x; в нашем примере мы получаем непосредственно х + х = 2х и, следовательно, если f (х) = х², то

Совершенно аналогично мы можем доказать, что в случае функции f(х) = х³ мы будем иметь f' (х) = 3х².

В самом деле, отношение

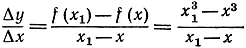
может быть упрощено по формуле

знаменатель Δх = х₁ - х сокращается, и мы получаем непрерывное выражение:

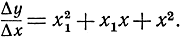
При стремлении х₁ к х это выражение стремится к сумме х² + х² + х²; в качестве предела получается выражение:

И вообще, для функции

где n - целое положительное, производная будет иметь вид:

Упражнение. Доказать этот результат. (Примените алгебраическую формулу

В качестве следующего примера, позволяющего непосредственно определить производную, рассмотрим функцию

Мы имеем:

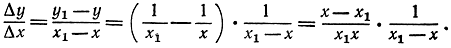
Сократим опять дробь и тогда получим:

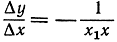
- выражение, опять-таки непрерывное в точке х₁ = х; в качестве предела мы, следовательно, будем иметь:

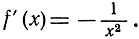
Само собой разумеется, что в данном случае ни производная, ни сама функция не определены в точке х = 0.

Упражнение. Доказать аналогичным способом, что функция имеет производную 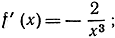функция 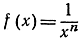имеет производную 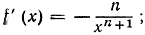функция f(x) = (1 + x)ⁿ имеет производную f'(x) = n(1 + x)^n-1.

Продифференцируем теперь функцию

В качестве разностного отношения мы получаем:

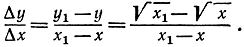
Воспользовавшись формулой x₁ - x = (√x₁ - √x)(√x₁ + √x), можно сократить знаменатель с первым из множителей и получить выражение, непрерывное в точке х₁ = х:

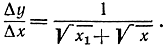
Переход к пределу дает

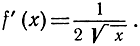
Упражнения. Доказать, что функция 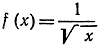имеет производную 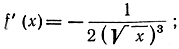доказать далее: