2. Производная как предел

Рассмотрение кривой y = f (x) только в одной ее точке Р (x, y) не позволяет вычислить наклон кривой в этой точке. Необходимо прибегнуть к предельному процессу, сходному с процессом вычисления площади. Этот предельный процесс является основой дифференциального исчисления. Рассмотрим на данной кривой другую точку Р₁, близкую к Р, с координатами х₁, y₁; обозначим прямую, проходящую через точки Р и Р₁, буквой t₁; эта прямая по отношению к нашей кривой является секущей, которая мало отличается от касательной в точке Р, если только точка Р₁ близка к точке Р. Обозначим угол между осью х и прямой t₁ буквой α₁. Заставим теперь х₁ стремиться к x; тогда точка Р₁ будет двигаться по кривой к точке Р и секущая t₁ будет приближаться к некоторому предельному положению, которое и есть не что иное, как касательная t к нашей кривой в точке х. Если буквой а обозначить угол между осью х и касательной t, то при х₁→х будем иметь

Касательная есть предел секущей, а наклон касательной есть предел наклона секущей^*.

^* (Наши обозначения здесь слегка отличаются от обозначений главы VI, поскольку там мы имели х→x₁, где x₁ постоянно. Никакой путаницы от этого изменения обозначений не произойдет.)

Хотя мы и не имеем явного выражения для наклона самой касательной t, зато наклон секущей t₁ дается формулой

наклон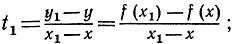

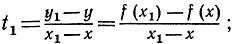
обозначая, как раньше, операцию образования разности символом Δ, мы получим

наклон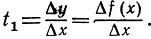

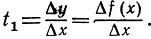
Наклон секущей t₁ есть "разностное отношение" - разность Δy значений функции, деленная на разность Δx значений независимого переменного. Сверх того, имеем наклон 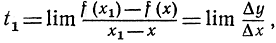где пределы вычисляются при х₁→;x, т. е. при Δх = х₁ - х → 0. Касательная t к данной кривой имеет наклон, равный пределу разностного отношения 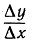при стремленииΔх = х₁ - хк нулю.

Первоначальная функция f(x) давала значение "высоты" различных точек кривой y = f(). Предположим теперь, что точка Р движется по кривой y = f (х). Тогда рассматриваемый наклон в точке Р будет представлять некоторую новую функцию от х, которую мы обозначим через f' (х) и назовем производной от функции f(x).

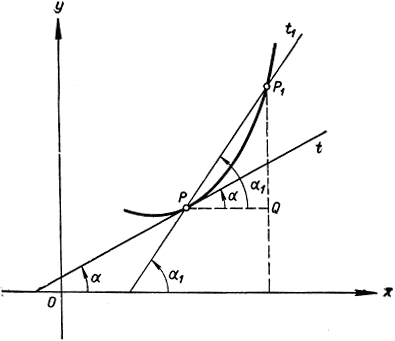
Рис. 268. Производная как предел

Предельный процесс, с помощью которого получена производная, называется дифференцированием функции f (х). Этот процесс есть такая операция, которая по определенному правилу сопоставляет данной функции f (х) некоторую другую функцию f' (х). Подобным же образом при определении самой функции f (х) было установлено правило, которое сопоставляло каждому значению переменного х некоторое значение функции f (х). Итак,

Слово "дифференцирование" объясняется тем обстоятельством, что f' (x) есть предел разности (differentia) f(x₁) - f (x), деленной на разность

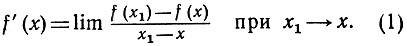
Другим часто употребляемым обозначением является

где символ D есть первая буква слова differentia, что значит "разность"; кроме того, для производной от функции y = f (x) существуют еще обозначения Лейбница

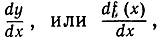
которые мы подвергнем обсуждению в § 4, "намекающие" на то, что производная получается как предел разностного отношения ^Δy/_Δx или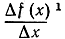

¹ (В русском издании в дальнейшем используются именно эти, общепринятые у нас обозначения.)

Условившись в том, что движение по кривой совершается в направлении возрастающих значений х, мы можем теперь заключить: то обстоятельство, что производная в некоторой точке положительна, f' (х) >0, означает подъем кривой (значения y возрастают). Напротив, то обстоятельство, что производная отрицательна, f' (х)<0, означает падение кривой (значения y убывают); наконец, если производная обращается в нуль, f' (х) = 0, то это означает горизонтальное направление кривой для соответствующего значения х. В точках максимума и минимума наклон должен быть равен нулю (рис. 269). Таким образом, решая уравнение

относительно х, мы можем найти положение максимумов и минимумов, как это было впервые сделано Ферма.

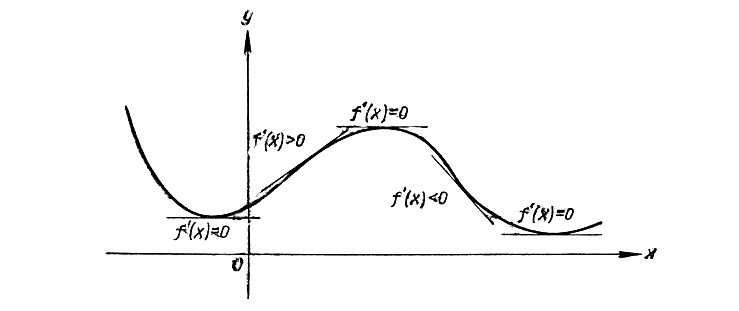
Рис. 269. Знак производной