§ 2. Производная

1. Производная как наклон

В то время как понятие интеграла своими корнями уходит в античную древность, другое основное понятие анализа- производная - было сформулировано только в XVII столетии знаменитым Ферма и другими. Сделанное Ньютоном и Лейбницем открытие органической связи между этими понятиями, казалось бы столь различными, способствовало небывалому развитию математической науки.

Ферма интересовался вопросом об определении наибольших и наименьших значений функции y = f (x). При изучении графика функции принято называть максимумом точку, расположенную выше всех других, а минимумом - точку, расположенную ниже всех других точек в ее окрестности. На рис. 191 на стр. 376 точка В является максимумом, точка С - минимумом. Естественно при нахождении максимума или минимума использовать понятие касательной к кривой. Предположим, что график кривой нигде не образует острых углов и не обладает другими особенностями и что в каждой точке он имеет определенное направление, определяемое касательной прямой. В точках максимума или минимума касательная к кривой y = f (x) должна быть параллельна оси х, в противном случае кривая около этих точек или поднималась бы, или опускалась бы. Это замечание побуждает нас заняться общим вопросом об определении направления касательной к кривой y = f (х) в любой точке Р этой кривой.

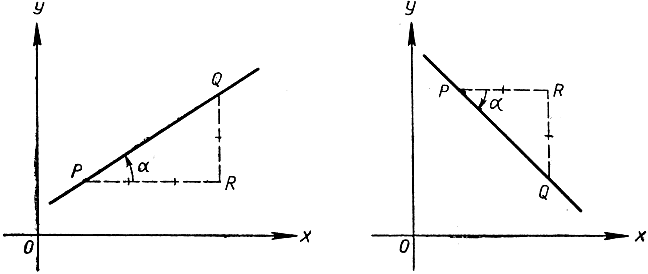
Рис. 267. Наклоны прямых

Чтобы характеризовать направление прямой в плоскости х, y, обыкновенно задается ее наклон, который представляет собой тангенс угла а между положительным направлением оси х и рассматриваемой прямой. Если Р есть некоторая точка прямой L, продвигаемся вправо от нее до некоторой точки R, а затем вверх или вниз до точки Q, лежащей на прямой, тогда наклон L равен tgα, т. е. 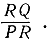Отрезок PR предполагается положительным, тогда как RQ - положительным или отрицательным в зависимости от того, будет ли он направлен вверх или вниз; таким образом, наклон дает нам подъем или падение на единицу длины по горизонтали (при перемещении по прямой слева направо). На рис. 267 наклон первой прямой равен ²/₃, в то время как наклон второй прямой равен -1.

Под наклоном кривой в точке Р мы подразумеваем наклон ее касательной в этой точке. Поскольку мы расположены принять понятие касательной как интуитивно данное, перед нами остается только задача - найти способ для вычисления наклона кривой. В настоящий момент мы станем именно на такую точку зрения: более тщательный анализ относящихся сюда проблем будет произведен в дополнении к этой главе.