
5. Правила "интегрального исчисления"
Важной ступенью в развитии интегрального исчисления явилось формулирование некоторых общих правил, с помощью которых более сложные задачи могут сводиться к более простым, а тем самым могут быть решены почти механически. Алгоритмический характер этих правил особенно ярко подчеркивается обозначениями Лейбница. Однако слишком сосредоточивать внимание на механизме решения задач при изучении анализа значило бы снижать содержание предмета и могло бы привести к пустой долбежке.
Некоторые простые правила интегрирования следуют сразу или из определения (6), или из геометрической интерпретации интегралов как площадей.
Интеграл от суммы двух функций равен сумме интегралов от этих двух функций. Интеграл от произведения функции на постоянное с равен произведению интеграла от функции на постоянное с. Эти два правила можно выразить одной формулой
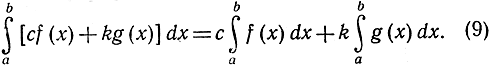
Доказательство следует непосредственно из определения интеграла как предела конечных сумм (5), поскольку соответствующая формула для суммы Sn, очевидно, справедлива. Это правило обобщается тотчас же на сумму более чем двух функций.
В качестве примера применения этого правила рассмотрим полином
f (х) = а0 + а1х + а2х2 + ... + аnхn,
коэффициенты которого а0, а1, ..., аn постоянны. Чтобы вычислить интеграл от функции f(x) в пределах от а до b, мы будем интегрировать почленно, согласно правилу. Применяя формулу (7), мы найдем
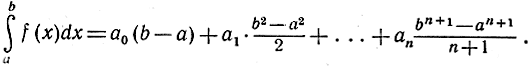
Другое правило, вытекающее со всей очевидностью как из аналитического определения интеграла, так и из его геометрической интерпретации, выражается формулой
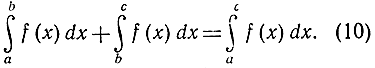
Кроме того, ясно, что наш основной интеграл равен нулю, если b равно а. Правило
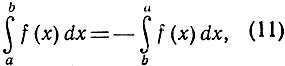
приведенное на стр. 438, не стоит в противоречии с последними двумя, поскольку оно получается из (10), при с = а.
Иногда бывает удобно использовать то обстоятельство, что значение интеграла не зависит от выбора наименования независимого переменного интегрируемой функции; например,
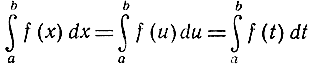
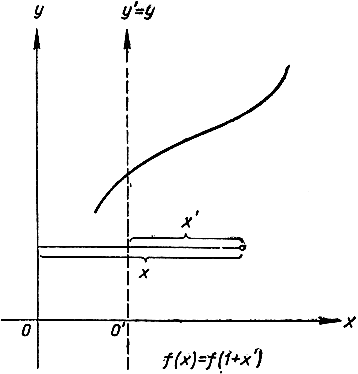
Рис. 265. Перемещение оси y
В самом деле, замена наименований f координат, к системе которых отнесен график функции, не меняет площади под данной кривой. Аналогичное замечание относится к тому случаю, когда производится некоторая замена в самой системе координат. Например, перенесем начало координат на одну единицу вправо из точки О в точку О', как показано на рис. 265, таким образом, что х будет заменено новой координатой х' по формуле х = 1 + х'. Уравнение кривой y = f(x) в новой системе координат примет вид y = f(1 + x') (например, 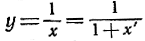 Данная площадь A под этой кривой, скажем, в пределах от х = 1 до х = b в новой системе координат будет площадью под кривой в пределах от х' = 0 до х' = b-1. Таким образом, будем иметь
Данная площадь A под этой кривой, скажем, в пределах от х = 1 до х = b в новой системе координат будет площадью под кривой в пределах от х' = 0 до х' = b-1. Таким образом, будем иметь
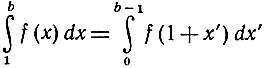
и, написав букву и вместо буквы х', получим
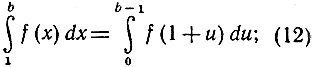
например,
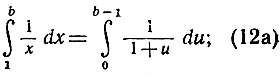
а для функции f (х) = х2 получим таким же образом
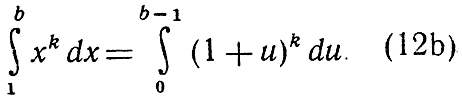
Аналогично
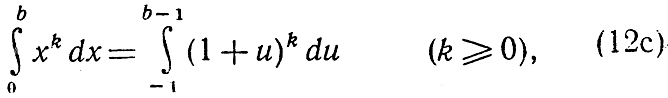
и, поскольку интеграл в левой части (12с) равен 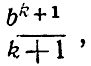 мы получим:
мы получим:
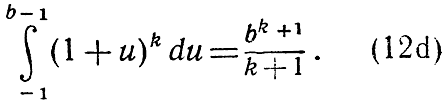
Упражнения.
- Вычислить интеграл от многочлена 1 + х + х2 + ... + хn в пределах от 0 до b.
- Доказать при n>0, что интеграл от функции (1 + x)n в пределах от -1 до z равен дроби
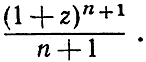
- Показать, что интеграл от xnsin x в пределах от 0 до 1 меньше, чем
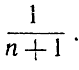 (Указание. Последняя величина есть значение интеграла от хn.)
(Указание. Последняя величина есть значение интеграла от хn.)
- Доказать непосредственно, а также пользуясь разложением по формуле бинома что интеграл от функции
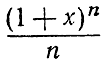 в пределах от -1 до z равен дроби
в пределах от -1 до z равен дроби 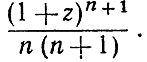
Следует упомянуть, наконец, два важных правила, которые выражаются посредством неравенств. Эти правила дают, правда, грубые, но все же полезные оценки для значения интегралов.
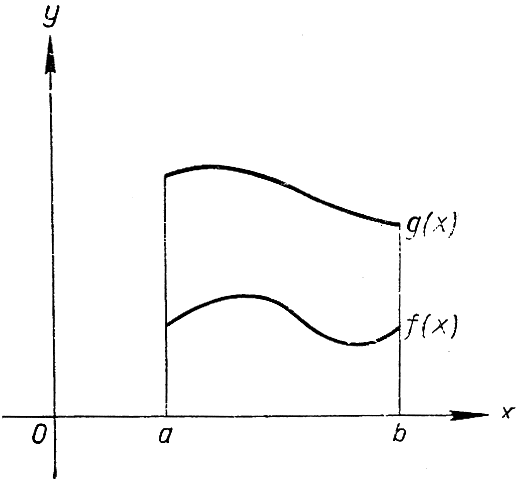
Рис. 266. Сравнение интегралов
Предположим, что b>a и что значения функции f(х) в промежутке от а до b нигде не превосходят значений другой функции g(x). Тогда мы имеем:
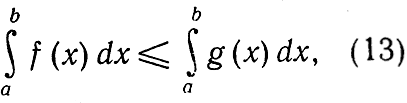
что непосредственно ясно или из рис. 266, или из аналитического определения интеграла. В частности, если функция g (x) равна M, т. е. является постоянной, то мы получаем:
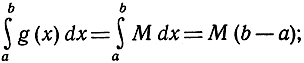
отсюда следует неравенство
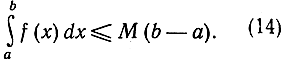
Если функция f (х) неотрицательна, то f (х) = |f (х)|. Если f (х)<0, то |f (х)|>f(x). Отсюда, полагая в неравенстве (13) g (х) = |f (x)|, мы получим полезную формулу:

Но, поскольку |- f(х)| = |f (х)|, мы имеем также формулу
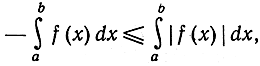
что дает вместе с формулой (15) более сильное неравенство, а именно
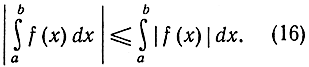
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'