4. Примеры интегрирования. Интегрирование функции x^r

До сих пор наши рассуждения об интеграле были чисто теоретическими. Возникает основной вопрос по поводу рассмотренного построения сумм S_n по общей установленной схеме и последующего перехода к пределу: ведет ли эта процедура к каким-либо осязаемым результатам в отдельных конкретных случаях? Конечно, решение этого вопроса потребует некоторых дополнительных рассуждений, приспособленных к тем специальным функциям f(х), от которых нужно найти интеграл.

Когда Архимед две тысячи лет тому назад вычислил площадь параболического сегмента, он выполнил то, что мы теперь называем интегрированием функции f(x) = x², притом чрезвычайно остроумным способом; в XVII столетии предшественники Ньютона и Лейбница успешно решили проблему интегрирования таких простых функций, как хⁿ, опять-таки с помощью специальных приемов. Только после рассмотрения большого числа конкретных примеров был найден общий подход к проблеме интегрирования на основе систематического метода, и таким образом область разрешимых задач была сильно расширена. В настоящей главе мы рассмотрим небольшое число отдельных конструктивных задач, принадлежащих к эпохе "праанализа", так как для операции интегрирования, понимаемой как предельный процесс, лучшей иллюстрации не придумаешь.

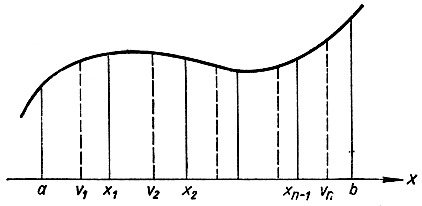
Рис. 262. Произвольность разбиения области определения функции при общем определении интеграла

a) Начнем с совершенно тривиального примера. Если y = f(x) является константой, например f(x) = 2, то, очевидно, интеграл понимаемый как площадь, равен 2(b-а), поскольку площадь прямоугольника равна произведению основания на высоту. Сравним этот результат с определенным интегралом. Если в формуле (5) мы подставим f(x_j) = 2 для всех значений j, то при любом значении n найдем, что

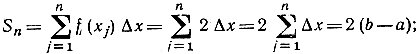
в самом деле,

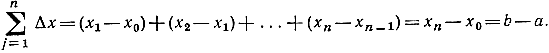
b) Почти так же просто проинтегрировать функцию f(x) = x. В этом примере интеграл 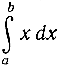является площадью трапеции (рис. 263), следовательно, согласно элементарной геометрии выразится формулой

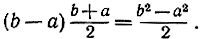
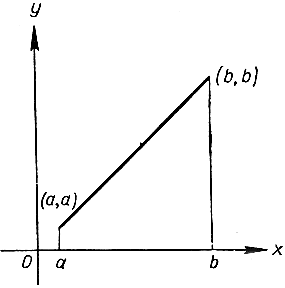
Рис. 263. Площадь трапеции

Этот же результат получается и из определения интеграла (6), в чем можно убедиться фактическим переходом к пределу без обращения к геометрическому представлению: если мы в формуле (5) положим f(x) = x, то сумма S_n примет вид:

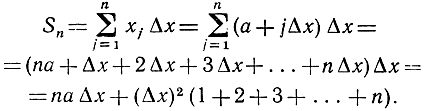
Применяя формулу для суммы арифметической прогрессии 1 + 2 + 3 + ... + n, выведенную на стр. 36, мы получим:

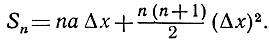
И так как

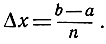
то отсюда следует

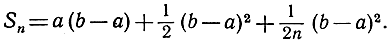
Пусть теперь n стремится к бесконечности; тогда переход к пределу даст результат

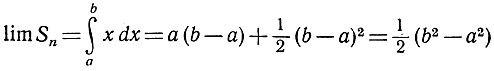
в полном соответствии с геометрической интерпретацией интеграла как площади.

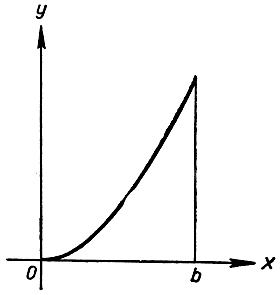
Рис. 264. Площадь под параболой

с) Менее тривиальным является интегрирование функции f(x) = x². Архимед употребил геометрический метод при решении эквивалентной задачи - нахождении площади сегмента параболы y = х². Здесь мы будем действовать аналитически, исходя из определения (6а). Чтобы упростить формальные выкладки, в качестве "нижнего предела" интеграла а выберем 0; тогда 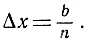Так как x_j = j*Δx и f(x_j) = j²*(Δx)², то для суммы S_n мы получим выражение

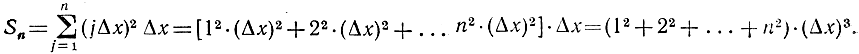
Теперь можно фактически вычислить предел. Применяя формулу

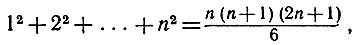
установленную на стр. 38, и заменяя Δx через 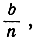мы получим:

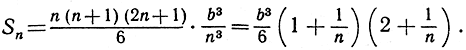
Это предварительное преобразование облегчает предельный переход: при неограниченном возрастании n обратная величина 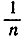стремится к нулю, и потому в качестве предела получается просто 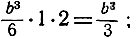следовательно, окончательный результат имеет вид:

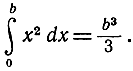
Применяя этот результат к площади от 0 до а, получим

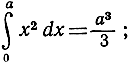
наконец, вычитание площадей дает

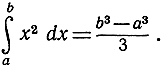
Упражнение. Тем же способом, употребляя формулу (5) со стр. 39, доказать, что

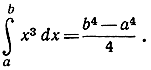
Применяя общие формулы для сумм 1^k + 2^k + ... + n^k k-x степеней целых чисел от 1 до n, можно было бы получить результат

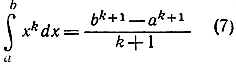
при любом целом положительном значений k.

^* Вместо того чтобы действовать этим путем, мы можем получить несколько проще даже более общий результат, воспользовавшись сделанным раньше замечанием о возможности вычислить интеграл и при неравностоящих точках деления. Мы выведем формулу (7) не только для любого целого положительного k, но и для любого положительного или отрицательного рационального числа

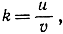
где u - целое положительное, а v - целое положительное или отрицательное число. Исключается только значение k = -1, при котором формула (7) теряет смысл. Предположим также, что 0<а<b.

Чтобы получить формулу (7), построим сумму S_n, выбирая точки деления х₀ = а, x₁, x₂, ..., x_n = b в геометрической прогрессии. Положим 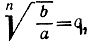так что 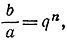и определим: x₀ = a, х₁ = aq, x₂ = aq², ..., x_n = aqⁿ = b. При таком выборе значений x_i, как мы увидим, предельный переход совершается особенно просто. Поскольку

мы будем иметь выражение

Так как каждый член содержит множители а^k (aq - а), то можно написать

Подставляя t вместо q^k+1, видим, что выражение в скобках является геометрической прогрессией 1 + t + t² + ... + t^n-1, сумма которой, как показано на стр. 38, равна 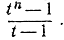Но

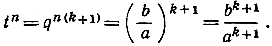
Таким образом,

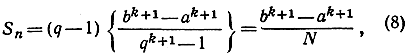
где

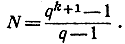
До сих пор n было фиксированным числом. Пусть теперь n возрастает; определим тогда предел, к которому стремится N. При возрастании n корень 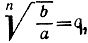стремится к 1 (см. стр. 357); поэтому и числитель, и знаменатель выражения N стремятся к нулю, что побуждает к осторожности. Предположим сначала, что k - целое положительное число: тогда можно осуществить деление на q - 1, и мы получим (см. стр. 127): N = q^k + q^k-1 + ... + q + 1. Если теперь n возрастает, так что q стремится к 1, а следовательно, и q², q³, ..., q^k также стремятся k-1, то N стремится к k+1. Но из этого вытекает, что S_n стремится к 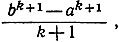что и требовалось доказать.

Упражнение. Доказать, что при любом рациональном k ≠ -1 остается в силе та же самая предельная формула N → k+1, а следовательно, сохраняется и результат (7). Сначала дать доказательство, следуя нашему образцу, в предположении, что k целое отрицательное. Затем, если 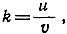положить 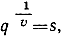откуда следует

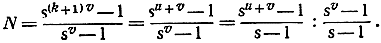
Если n возрастает, так что q и s стремятся к 1, то отношения в последней части равенства стремятся соответственно к u + v и к v, что в качестве предела для N снова дает

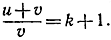
В § 5 мы увидим, каким образом с помощью мощных методов анализа можно упростить это длинное и несколько искусственное рассуждение.

Упражнение.

1. Проверить предшествующее интегрирование x^k для случаев
   
   
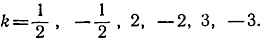
2. Вычислить значения интегралов:
   
   
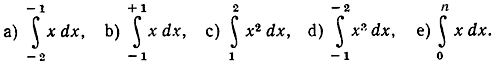
3. Найти значения интегралов:
   
   
   (Указание. Рассмотреть графики функций под знаком интеграла, принять во внимание их симметрию по отношению к оси х = 0 и интерпретировать интегралы как площади.)
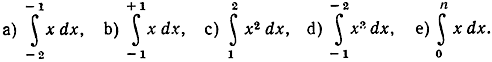
4. ^* Проинтегрировать sin х и cos х в пределах от 0 до b, подставляя h вместо Δх и применяя формулы со стр. 528.
5. Проинтегрировать f (х) = х и f (х) = х² в пределах от 0 до b, производя раздробление на равные части и в формуле (6а) выбирая значения
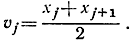
6. ^* Пользуясь результатом (7) и определением интеграла с равными значениями для Δх, доказать предельное соотношение
   
   
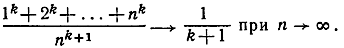
   (Указание. Положить 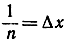и показать, что рассматриваемый предел равен интегралу )
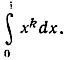7. ^* Доказать, что при n→∞ справедливо следующее предельное соотношение:
   
   
   (Указание. Напишите эту сумму так, чтобы ее предел являлся некоторым интегралом.)
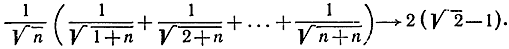
8. Вычислить площадь параболического сегмента, ограниченного дугой Р₁Р₂ и хордой Р₁Р₂ параболы y = ах², выражая результат через координаты точек Р₁ и Р₂.