3. Общие замечания о понятии интеграла. Общее определение

В нашем геометрическом определении интеграла как площади мы явно предполагали, что функция f(x) во всем промежутке интегрирования [а, b] неотрицательна, т. е. что никакая часть графика не лежит под осью х. В аналитическом же определении интеграла как предела последовательности сумм S_n такое предположение является излишним. Мы просто возьмем малые количества f(x_j)Δx, составим их сумму и перейдем к пределу; эта процедура остается имеющей вполне определенный смысл и в том случае, если некоторые или все значения f(x_j) отрицательны. Интерпретируя это геометрически с помощью площадей (рис. 261), мы приходим к заключению, что интеграл от f(x) представляет собой алгебраическую сумму площадей, ограниченных графиком и осью х, причем площади, лежащие под осью х, считаются отрицательными, остальные - положительными.

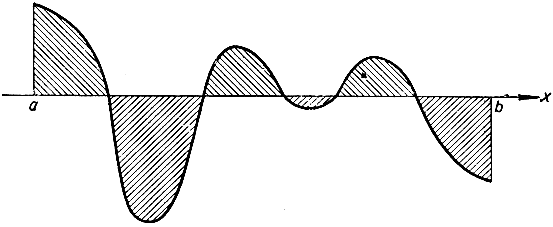
Рис. 261. Положительные и отрицательные площади

Может случиться, что в тех или иных случаях мы придем к интегралам 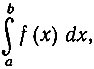в которых b меньше, чем а, так что 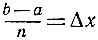окажется отрицательным числом. Тогда в нашем аналитическом определении члены вида f(x_j)Δx будут отрицательными, если f(x_j) положительно, а Ах отрицательно, и т. д. Другими словами, величина этого интеграла будет только знаком отличаться от величины интеграла в пределах от b до а. Таким образом получаем следующее простое свойство интеграла:

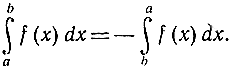
Далее, нужно подчеркнуть, что значение интеграла не меняется и в том случае, если точки деления х_j не будут выбираться равностоящими, другими словами, если разности Δx = х_j+1 - x_j не будут одинаковы. Мы можем выбрать x_j произвольно, и тогда разности Δx_j = х_j+1 - x_j должны быть различаемы с помощью соответствующих значков. Даже в этом предположении сумма

а также сумма

будут стремиться к одному и тому же пределу, именно к значению интеграла 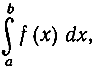если только мы позаботимся о том, чтобы с возрастанием n все разности Δx_j = x_j+1 - x_j стремились к нулю таким образом, чтобы наибольшая из них (при данном значении n) стремилась к нулю, когда n неограниченно возрастает.

Окончательное определение интеграла дается с помощью формулы

при n→∞. Под знаком суммы число υ_j может обозначать любую точку в промежутке x_j≤υ_j≤x_j+1, и единственное ограничение, касающееся способа разбиений основного промежутка, заключается в том, чтобы наибольшая из разностей Δx_j = х_j+1 - x_j стремилась к нулю, когда n стремится к бесконечности.

Существование предела (6а) не требует доказательства, если мы допустим как само собой разумеющееся понятие "площади под кривой", а также и возможность приближения этой площади с помощью прямоугольников. И все же, как это выяснится из дальнейших рассуждений (стр. 502), более глубокий анализ показывает, что для того, чтобы определение интеграла было логически совершенным, желательно и даже необходимо доказать существование этого предела независимо от первоначального геометрического представления о площади и притом какова бы ни была непрерывная функция f(x).