2. Интеграл

Первым основным понятием анализа является понятие интеграла. В этой главе мы будем понимать интеграл как площадь под кривой, выраженную с помощью предела. Пусть дана непрерывная положительная функция y = f(x), например y = х² или y = 1 + cosx; рассмотрим область, ограниченную снизу отрезком оси от некоторой точки а до некоторой точки Ь, причем а меньше b, справа и слева - перпендикулярами к оси - х в этих точках, а сверху - кривой y = f(x). Цель наша - вычислить площадь А этой области.

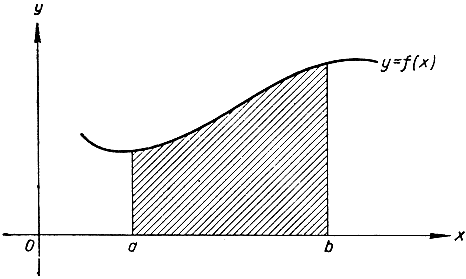
Рис. 259. Интеграл как площадь

Так как такая площадь не может быть, вообще говоря, разбита на прямоугольники или треугольники, то непосредственно нельзя указать точную математическую формулу, которая была бы пригодна для вычисления площади A. Но мы можем находить приближенные значения для А и, следовательно, представить А как предел следующим образом: разделим промежуток от х = а до х = b на некоторое число маленьких частных промежутков, восставим перпендикуляры в каждой точке деления, и каждую полоску области под кривой заменим прямоугольником, высоту которого выберем произвольно между наибольшей и наименьшей ординатами кривой в этой полоске. Сумма S площадей этих прямоугольников даст приближенное значение истинной площади "под" данной кривой. Точность этого приближения тем лучше, чем больше число прямоугольников и чем меньше ширина каждой отдельной полоски. Итак, мы принимаем следующее определение интересующей нас площади: Если мы построим последовательность

приближений прямоугольниками площади кривой, причем основание самого широкого прямоугольника в сумме S_n стремится к нулю, когда n возрастает, то последовательность (1) стремится к пределу А:

и этот предел A, представляющий собой площадь под данной кривой, не зависит от того, каким именно образом выбрана последовательность (1), раз только основания прямоугольников неограниченно уменьшаются. (Например, S_n может получаться из S_n-1 путем прибавления одной или нескольких новых точек к прежним, определяющим S_n-1, или же выбор точек деления для S_n может совершенно не зависеть от выбора точки для S_n-1.) Площадь А данной области, выраженную указанным предельным переходом, мы называем по определению интегралом от функции f(x) в пределах от а до b. Вводя специальный символ - знак интеграла, запишем это так:

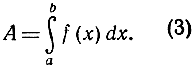
Символ ∫, значок dx и название "интеграл" были введены Лейбницем, чтобы намекнуть на способ получения этого предела. Чтобы объяснить это обозначение, мы еще раз, с большими подробностями, повторим процесс приближения площади A. И в то же время аналитическая формулировка перехода к пределу позволит отбросить стесняющие предположения f(x)≥0 и b>а и в конце концов избавиться от первоначальной интуитивной концепции интеграла как "площади под кривой" (это будет сделано в дополнении, § 1).

Разделим промежуток от а до b на n маленьких частных промежутков, которые только ради простоты мы будем предполагать имеющими одинаковую длину 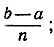обозначим точки деления следующим образом:

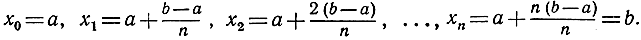
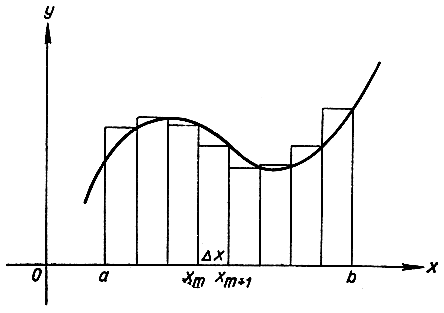
Рис. 260. Приближение площади ступенчатой фигурой

Введем для обозначения величины 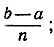разности между двумя последовательными значениями х символ Δх (читается "дельта икс"):

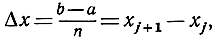
где символ Δ обозначает просто "разность". Это оперативный символ, который нельзя рассматривать как числовой множитель. За высоту каждого приближающего прямоугольника мы можем принять значение y = f(x) в правой крайней точке соответствующего промежутка. Тогда сумма площадей прямоугольников будет равна

или, сокращенно:

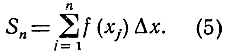
Символ 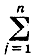(читается "сумма по j от 1 до n") обозначает сумму всех выражений, получаемых, когда j последовательно пробегает значения 1, 2,..., n.

Употребление символа ∑ для выражения результата суммирования в сжатой форме можно иллюстрировать следующими примерами:

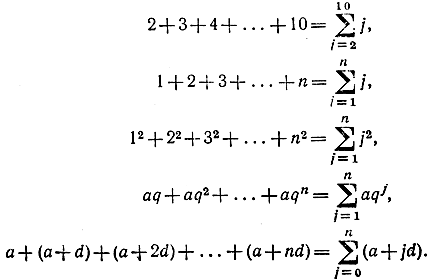
Построим теперь последовательность таких приближений S_n, в которых n возрастает неограниченно, так что число членов в каждой из сумм (5) стремится к бесконечности, в то время как каждый отдельный член f(x_j)Δx стремится к 0 вследствие присутствия множителя 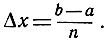При возрастании n эта сумма стремится к площади А:

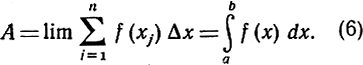
Лейбниц символизировал этот предельный переход от приближающих сумм S_n к пределу А заменой знака суммирования ∑ через &∫, а символа разности Δ символом d. (Во времена Лейбница знак суммирования ∑ писался обычно в виде S, и символ ∫ представляет собой просто стилизацию буквы S.) Несмотря на то что символика Лейбница хорошо намекает на способ, каким был получен интеграл, не следует придавать слишком большого значения тому, что является лишь чисто условным приемом обозначения предела. В ранние дни анализа, когда отчетливого понятия о пределах еще не существовало и необходимость предельного перехода часто упускалась из виду, многие пытались объяснить смысл интеграла, говоря, что "конечное приращение Δх заменено бесконечно малой величиной dx, а сам интеграл есть сумма бесконечно большого числа бесконечно малых слагаемых f(x)dx". Хотя "бесконечно малое" имеет известную притягательность для умов, имеющих склонность к философским спекуляциям, ему нет и не может быть места в современной математике. Никакой полезной цели нельзя достигнуть, окружая ясное понятие интеграла туманом не имеющих смысла фраз. Но даже сам Лейбниц иногда поддавался соблазнительному воздействию своих символов: в самом деле, они работают так, как если бы обозначали сумму "бесконечно малых" величин, с которыми можно до некоторой степени оперировать, как с обыкновенными величинами. Даже само слово "интеграл" было создано для того, чтобы обозначить, что "всё", т. е. "полная" площадь A, составлено из "бесконечно малых" частиц f(x)dx. Как бы то ни было, прошло около сотни лет после Ньютона и Лейбница, прежде чем было ясно осознано, что истинной основой определения интеграла является понятие предела, и ничего больше. Твердо став на эту точку зрения, мы избегнем всякой неясности, всех трудностей и всех нелепостей, которые вызывали такое смущение в ранний период развития анализа.