§ 1. Интеграл

1. Площадь как предел

Для того чтобы вычислить площадь плоской фигуры, мы в качестве единицы площади выбираем квадрат со стороной, равной единице длины. Если единицей длины является сантиметр, соответствующей единицей площади будет квадратный сантиметр, т. е. квадрат, длина стороны которого равна сантиметру. С помощью этого определения весьма легко вычислить площадь прямоугольника. Если длины двух смежных сторон, измеренные в линейных единицах, представляются числами р и q, то площадь прямоугольника равна pq квадратных единиц, или, короче, площадь равна произведению pq. Это справедливо для любых р и q как рациональных, так и иррациональных. В случае рациональных значении р и q мы получаем этот результат, выполняя замену 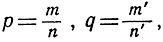где m, n, m', n' - целые числа. 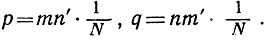После этого мы находим общую меру обеих сторон - таким образом, что Наконец, мы разбиваем прямоугольник на мелкие квадратики со стороной 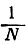и с площадью 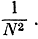Всего таких квадратиков будет nm'*mn', и общая площадь равна 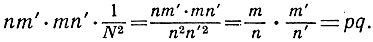Для случая р и q иррациональных тот же результат получится, если сначала заменим р и q соответственно приближающими их рациональными числами р_r и q_r, а затем заставим р_r и q_r стремиться к р и q.

Геометрически очевидно, что площадь треугольника равна половине площади прямоугольника с тем же основанием b и высотой h; таким образом, площадь треугольника выражается хорошо известной формулой 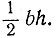Любая плоская область, ограниченная одной или несколькими ломаными, может быть разбита на треугольники; таким образом, ее площадь может быть получена как сумма площадей этих треугольников.

Потребность в более общем методе вычисления площадей возникает в связи с вопросом о вычислении площадей фигур, ограниченных уже не ломаными, а кривыми. Каким образом станем мы определять, например, площадь круга или сегмента параболы? Этот капитальной важности вопрос, с решением которого связано обоснование интегрального исчисления, рассматривался с очень давних пор: еще в III в. до нашей эры Архимед вычислял площади подобного рода с помощью процедуры "исчерпания". Попробуем вместе с Архимедом и великими математиками до времен Гаусса стать на "наивную" точку зрения, согласно которой криволинейные площади являются интуитивно данными сущностями, так что вопрос стоит не об определении понятия площади, а о вычислении площади (см., однако, анализ этого понятия, произведенный на стр. 502). В рассматриваемую криволинейную область впишем многоугольник, ограниченный ломаной линией и обладающий прекрасно определенной площадью. Выбирая новый многоугольник такого же типа, включающий первый, мы получим лучшее приближение для площади заданной области. Продолжая таким образом, мы постепенно "исчерпаем" всю область и получим искомую площадь как предел площадей надлежащим образом подобранной последовательности вписанных многоугольников с возрастающим числом сторон. Так может быть вычислена площадь круга с радиусом 1; ее числовое значение обозначается символом я.

Эту общую схему Архимед провел до конца в случае круга и в случае параболического сегмента. В течение XVII столетия было с успехом разобрано много других примеров. В каждом случае само вычисление предела ставилось в зависимость оттого или иного остроумного приема, специально подобранного для каждой отдельной задачи. Одним из главных достижений анализа была замена этих специальных искусственных процедур одним общим и мощным методом.