4. Геодезические линии на сфере. Минимаксы

Во введении к этой главе была упомянута проблема нахождения "геодезических линий" - кратчайших дуг, соединяющих две данные точки на некоторой поверхности.. На сфере, как показывается в элементарной геометрии, такими линиями являются дуги больших кругов. Пусть Р и Q - две точки на сфере (не являющиеся диаметрально противоположными) и с - меньшая из двух дуг большого круга, проходящего через Р и Q. Тогда возникает вопрос: чем же является другая, большая из двух дуг с' того же круга. Конечно, минимума расстояния между точками Р и Q она не дает, но не дает и максимума, так как легко понять, что можно провести на сфере сколь угодно длинные дуги, соединяющие две данные точки. Оказывается, что по отношению к рассматриваемой проблеме дуга с' представляет собой минимакс, "седловую точку". Вообразим произвольную переменную точку S на сфере и поставим задачей найти кратчайший путь от Р к Q, проходящий через S. Конечно, минимум расстояния в такой постановке проблемы дается "ломаной" дугой, состоящей из двух дуг больших кругов PS и SQ. А затем постараемся найти такое положение точки S, при котором наименьшее расстояние PSQ было бы максимальным. Тогда получаем следующее решение вопроса: точка S должна быть такова, чтобы ломаная PSQ была более длинной дугой с' большого круга PQ. Можно видоизменить проблему, поставив сначала вопрос о кратчайшем пути на сфере от точки Р к точке Q, проходящем через n наперед заданных точек S₁, S₂, ..., S_n, а затем определяя точки S₁, S₂, ..., S_n таким образом, чтобы минимальная длина была насколько возможно большой. Решением такой задачи служит путь по большому кругу, проходящему через Р к Q, но обвивающийся вокруг сферы таким образом, чтобы пройти через точки, диаметрально противоположные Р и Q ровно n раз.

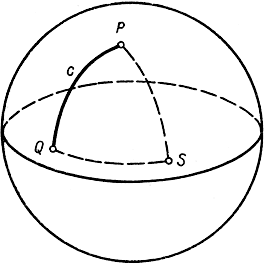
Рис. 239. Геодезические линии на сфере

Эта минимаксная проблема является типичным примером обширного класса вопросов из области вариационного исчисления, с полным успехом изученных в последнее время с помощью методов, предложенных Морзом и другими авторами.