3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли

Ранний метод, примененный к решению проблемы о брахистохроне Якобом Бернулли, может быть изложен с привлечением сравнительно скромных математических средств. Возьмем в качестве исходного тот известный из механики факт, что материальная частица, начинающая свой путь в точке А с нулевой скоростью и затем скользящая вниз по произвольной кривой С, приходит в некоторую точку Р со скоростью, пропорциональной величине √h, где h есть отсчитываемое по вертикали расстояние точки Р от точки А; иначе говоря, мы имеем зависимость υ = c√h, где с - постоянный коэффициент. Подвергнем рассматриваемую задачу легкому видоизменению. Разобьем мысленно пространство на множество горизонтальных слоев, каждый толщиной d, и предположим на минуту, что скорость нашей частицы меняется не непрерывно, а небольшими скачками - при переходе от слоя к слою; именно в первом слое, прилежащем непосредственно к точке A, скорость равна с√d, во втором с√2d, наконец в n-м 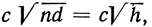где h - расстояние Р от A, отсчитываемое по вертикали (рис. 238). При такой постановке задачи мы имеем дело с конечным числом переменных. В пределах каждого слоя путь частицы должен быть прямолинейным. Вопрос о существовании экстремума не возникает; решение должно даваться ломаной линией; нужно только определить ее углы при вершинах.

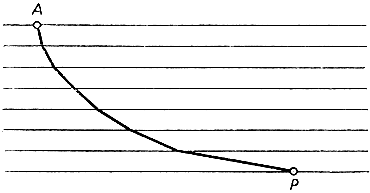
Рис. 238. К проблеме брахистохроны

Согласно минимальному принципу простого преломления в каждой паре соседних слоев движение от Р к R через Q таково, что при фиксированных Р и R точка Q соответствует наименьшему времени пути. Отсюда вытекает следующий "закон преломления":

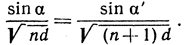
Повторное применение этого рассуждения приводит к цепи равенств

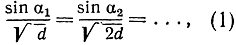
где α_n обозначает угол между направлением пути в n-м слое и вертикалью.

Затем Бернулли предполагает, что толщина слоев d, неограниченно уменьшаясь, стремится к нулю, причем ломаная траектория, решающая приближенную проблему, в пределе переходит в искомую кривую, решающую основную проблему. При этом предельном переходе равенства (1) сохраняются, и потому Бернулли делает заключение: если α обозначает угол, который в произвольной точке Р кривой С траектория брахистохронного движения делает с вертикалью, а h - расстояние от А до Р, рассчитываемое по вертикали, то выражение 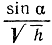должно сохранять постоянное значение во всех точках Р кривой С. Легко показать, что указанное свойство характеризует циклоиду.

Бернуллиево "доказательство" представляет собой типичный пример остроумного и плодотворного математического рассуждения, которое в то же время нельзя назвать безукоризненно строгим. В нем содержится несколько неявно принятых допущений, оправдание которых было бы сложнее и пространнее, чем само рассуждение. Так, с одной стороны, не доказывается само существование решения С, с другой - постулируется без достаточных математических оснований, что решение приближенной проблемы является приближенным решением основной проблемы. Вопрос о внутренней ценности такого рода эвристических (наводящих) построений заслуживает внимательного рассмотрения, но завел бы нас слишком далеко в сторону.