2. Вариационное исчисление. Принцип Ферма в оптике

Среди различных методов, с помощью которых решение брахистохрон-ной проблемы было найдено братьями Бернулли и другими учеными, мы выберем и изложим здесь один из самых ранних в историческом смысле. Первые предложенные методы носили более или менее специальный характер, будучи более приспособлены к специфическим задачам. Но очень скоро Эйлер и Лагранж (1736-1813) разработали более общие методы для решения экстремальных проблем, в которых независимым элементом является не одна или несколько (в конечном числе) числовых переменных, а кривая, или функция в целом, или даже система кривых (функций). Новый метод решения подобного рода проблем получил название вариационного исчисления.

Дать здесь изложение этой ветви математики в ее техническом аспекте или же проанализировать сколько-нибудь глубоко отдельные относящиеся сюда проблемы не представляется возможным. Вариационное исчисление имеет множество применений в физических теориях. Было замечено с давних пор, что явления природы часто следуют тем или иным экстремальным принципам. Как мы уже видели, Герон Александрийский усмотрел, что отражение светового луча плоским зеркалом хорошо описывается на основе принципа минимума. Ферма - уже в XVII столетии - сделал следующий шаг, заметив, что и закон преломления света также прекрасно выражается в терминах минимального принципа. Отлично известно, что при переходе светового луча из одной однородной среды в другую путь его изменяет направление. Так, световой луч, идущий из точки Р (рис. 237) в верхней среде, где скорость равна и, В точку R в нижней среде, где скорость есть ω, совершит ломаный путь PQR. Снеллиус (1591-1626) сформулировал найденный им эмпирическим путем закон, согласно которому путь состоит из двух прямолинейных отрезков PQ и QR, образующих с нормалью углы α и α', причем 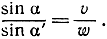С помощью дифференциального исчисления Ферма установил, что этот путь как раз обладает тем свойством, что время, нужное для прохода луча из Р в R, минимально, т. е. меньше, чем понадобилось бы при прохождении по любому иному пути. Таким образом, спустя шестнадцать столетий геронов закон отражения света был дополнен подобным ему и столь же важным законом преломления.

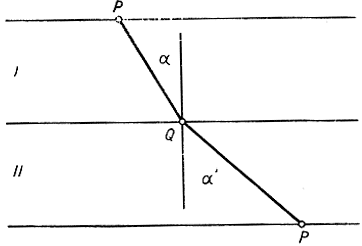
Рис. 237. Преломление светового луча

Ферма обобщил формулировку этого закона, распространяя его на случай кривых поверхностей раздела между двумя средами, каковы, например, сферические поверхности линз. Оказывается, что и в этом случае световой луч следует пути, обладающему тем свойством, что время, нужное для его прохождения, меньше, чем понадобилось бы при выборе любого другого пути. Наконец, Ферма рассмотрел и случай произвольной оптической системы, в которой скорость света меняется по определенному закону от точки к точке, например, так, как это происходит в атмосфере. Он разделил непрерывную неоднородную среду на тонкие слои, в каждом из которых скорость света приблизительно постоянна, и представил себе новую, воображаемую среду, в которой скорость света действительно постоянна в пределах каждого слоя. При таких условиях можно было применять прежний принцип при переходе от каждого слоя к следующему. Затем, допуская, что толщина каждого слоя стремится к нулю, он получил общий принцип геометрической оптики (известный ныне под именем принципа Ферма): в неоднородной среде световой луч, идущий от одной точки к другой, следует по такому пути, что время, нужное для его прохождения, меньше, чем понадобилось бы при прохождении любого иного пути. Этот принцип оказался в высшей степени полезным не только теоретически, но и практически. В геометрической оптике, оперируя техническим аппаратом вариационного исчисления, пользуются этим принципом как основным орудием при расчетах систем линз.

Минимальные принципы стали затем господствующими и в других областях физики. Так, было замечено, что устойчивое равновесие механической системы бывает достигнуто при таком расположении, при котором "потенциальная энергия" минимальна. Рассмотрим, например, свободно изгибаемую однородную цепь, подвешенную за два ее конца и предоставленную действию силы тяжести. Тогда цепь займет именно такое положение, при котором ее потенциальная энергия будет наименьшей. В указанном примере потенциальная энергия зависит от высоты центра тяжести относительно некоторой постоянной оси. Кривая, образованная свободно подвешенной цепью, называется цепной линией и по внешнему виду несколько напоминает параболу.

Не только закон равновесия, но и законы движения подчиняются экстремальным принципам. Отчетливые представления об этих принципах впервые возникли у Эйлера, тогда как люди, склонные к спекулятивным размышлениям философского и мистического характера, как например Мопертюи (1698-1759), не были способны дать точные математические формулировки и ограничивались смутными высказываниями по поводу "божественного регулирования физических явлений общими принципами наивысшего совершенства". Эйлеровы вариационные принципы в области физики, вновь открытые и обобщенные ирландским математиком Гамильтоном (1805-1865), стали впоследствии могущественнейшим орудием в таких областях, как механика, оптика, электродинамика, самые разнообразные технические науки. Физические теории недавнего происхождения - теория относительности и квантовая теория - полны примеров, обнаруживающих значение методов вариационного исчисления.