*§ 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой

Решение экстремальных проблем принимает своеобразные черты, если область значений переменного подчинена тем или иным граничным условиям. Теорема Вейерштрасса (утверждающая, что в компактной области непрерывная функция принимает наибольшее и наименьшее значения) не исключает возможности того, что эти экстремальные значения достигаются на границе области. В качестве простого, почти тривиального примера может служить функция u = х. Если х не подчинено никаким ограничениям и может изменяться от -∞ до +∞, то область В независимого переменного есть вся действительная ось; отсюда легко понять, что функция u = х нигде не принимает ни наибольшего, ни наименьшего значения. Но если область В ограничена, например, неравенством 0≤x≤1, то налицо имеется и наибольшее значение 1, достигаемое на правом конце промежутка, и наименьшее значение 0, достигаемое на левом. Но этим экстремальным значениям не соответствует "вершина" или "впадина" графика рассматриваемой функции. Иначе говоря, это экстремумы относительно не "двусторонней" окрестности; оставаясь на концах промежутка, они смещаются при расширении рассматриваемого промежутка. Если речь идет о настоящей "вершине" или "впадине" кривой, то экстремальный характер относится к полной окрестности рассматриваемой точки: небольшие сдвиги границы промежутка никак не влияют на экстремум. Такого рода экстремум сохраняется даже при свободном изменении переменного во всей области В или по крайней мере в некоторой достаточно малой окрестности точки. При самых разнообразных обстоятельствах поучительно уяснить себе различие между "свободными" и' "граничными" экстремумами. В случае функций одной переменной это различие, правда, стоит в тесной связи со свойствами монотонности, или немонотонности функции и потому не приводит к каким-нибудь особенно интересным замечаниям. Но стоит остановиться несколько внимательнее на условиях достижения экстремума на границе области изменения в случае функций многих переменных.

Рассмотрим, например, проблему Шварца, касающуюся треугольника. Область изменения трех независимых переменных состоит здесь из троек точек Р, Q, R, лежащих соответственно на сторонах треугольника AВС. Решение проблемы носит альтернативный характер: или минимум достигается при условии, что каждая из трех независимо движущихся точек Р, Q, R находится внутри соответствующей стороны треугольника (и тогда задача решается высотным треугольником), или же минимум достигается "на границе", когда какие-то две из точек Р, Q, R совпадают с общим концом двух смежных сторон (и тогда минимальный "треугольник" есть не что иное, как дважды считаемая высота данного треугольника). Характер решения - тот или иной, смотря по тому, какая из возможностей имеет место.

В проблеме Штейнера, относящейся к трем "деревням", область изменения точки Р есть вся плоскость, причем данные три точки A, В, С могут считаться граничными. И в этом случае возникают две возможности, дающие решение существенно различного характера: или минимум достигается внутри треугольника ABC (и тогда около точки Р возникают три равных угла), или он достигается в одной из вершин - граничных точек области изменения. Подобные альтернативы имеют место и для дополнительной проблемы.

Рассмотрим, наконец, в качестве последнего примера изопериметрическую проблему с добавочными граничными условиями. Мы установим при этом замечательную связь между изопериметрической проблемой и проблемой Штейнера и, помимо того, встретимся с простейшим примером экстремальной проблемы нового типа. В исходной изопериметрической проблеме замкнутая кривая данной длины, играющая роль независимого переменного, может быть свободно деформируема, как угодно отклоняясь от окружности, и любая получаемая кривая является "допустимой"; таким образом, окружность дает настоящий свободный минимум. Видоизмененная проблема содержит дополнительное требование: допустимые кривые С должны заключать внутри себя данные точки Р, Q, R (или должны проходить через них); как и раньше, площадь А считается заданной, и предлагается минимизировать длину L. В этом примере мы имеем "граничное" условие в настоящем смысле слова.

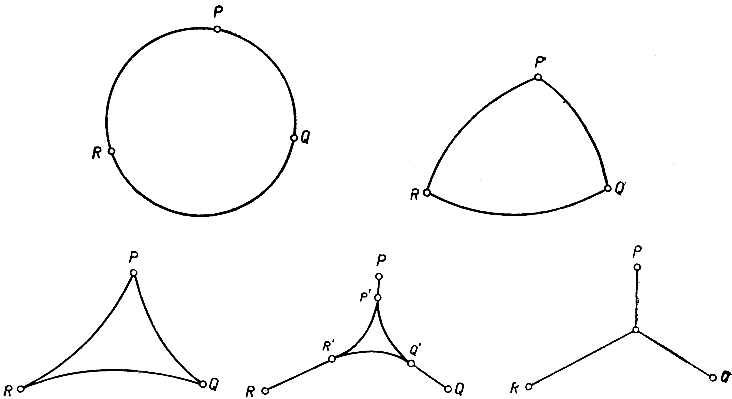
Рис. 231-235. Изопериметрические фигуры, в пределе дающие решение проблемы Штейнера

Ясно, что при достаточно большом значении А три точки Р, Q, R не оказывают на решение проблемы никакого влияния. В самом деле, если только А больше (или равно) площади круга, описанного около треугольника PQR, решение дается просто-напросто окружностью, охватывающей эти точки. Но что получается в противном случае? Укажем только результаты, оставляя в стороне детали доказательства, впрочем, вполне элементарного. Итак, постараемся охарактеризовать решение проблемы, предполагая, что данное числовое значение А постепенно становится меньше и, наконец, обращается в нуль. Как только А делается меньше, чем площадь описанного крута, изопериметрическая окружность превращается в три круговые дуги одного и того же радиуса, образующие выпуклый треугольник с вершинами Р, Q, R (рис. 232). Этот треугольник и дает решение проблемы; он определяется полностью числовым значением А. При убывании А радиус дуг увеличивается, и дуги выпрямляются; когда А становится равным площади треугольника PQR, этот самый треугольник и дает решение. Если А становится еще меньше, то снова получаются треугольники, составленные из круговых дуг одного и того же радиуса, но с выпуклостью, обращенной внутрь треугольника, с вершинами - или, лучше сказать, "рожками" - в точках Р, Q, R (рис. 233). При дальнейшем убывании А наступит момент, когда две круговые дуги, смыкающиеся у одной из данных точек, например R, станут касательными друг к другу. Еще далее, треугольники указанного типа уже перестанут быть возможными, и тогда обнаруживается новое явление: решение, как и перед тем, дается вогнутым треугольником, составленным из круговых дуг, но один из "рожков" R' отделяется от точки R, и решение тогда состоит из кругового треугольника PQR' с добавлением "дважды считаемого" (от R' к R и обратно) прямолинейного отрезка RR'. Этот отрезок касается двух круговых дуг, смыкающихся в точке R'. Когда А убывает еще дальше, "рожки" отделяются и у прочих вершин. При достаточно малых положительных значениях А мы будем иметь равносторонний треугольник, составленный из трех круговых дуг одного и того же радиуса, касающихся друг друга в вершинах Р', Q', R', с добавлением трех "дважды считаемых" отрезков Р'Р, Q'Q, R'R (рис. 234). Наконец, при обращении А в нуль названный треугольник обращается в точку, и мы получаем решение проблемы Штейнера, которая, таким образом, оказывается предельным случаем обобщенной (указанным выше способом) изопериметрической проблемы.

Если Р, Q, R образуют тупоугольный треугольник с углом в 120 или больше, то при стремлении А к нулю в пределе также получается решение проблемы Штейнера, так как круговые дуги в конце концов сливаются со сторонами тупого угла. Аналогичным образом, путем предельного перехода от изопериметрической проблемы, могут быть получены и решения обобщенной проблемы Штейнера (см. рис. 216-218 на стр. 393).