§ 8. Изопериметрическая проблема

Что среди всех замкнутых кривых данной длины именно окружность охватывает наибольшую площадь,- это один из "очевидных" фактов математики, строгое доказательство которых возможно только на основе новейших методов. Несколько остроумных способов доказательства этой теоремы предложил Штейнер; мы рассмотрим одно из его доказательств.

Начнем с допущения, что решение проблемы существует. Приняв это, предположим, что это решение осуществляется некоторой кривой С, имеющей длину L и охватывающей максимальную площадь. Легко доказать, что кривая С выпуклая: это значит, что прямолинейный отрезок, соединяющий любые две точки С, лежит целиком внутри или на С. Если бы кривая С не была выпуклой, то, как показано на рис. 226, можно было бы указать отрезок OP, конечные точки которого находились бы на С, а сам он был бы вне С. Дуга OQ'P - отражение дуги OQP относительно ОР - образовывала бы вместе с дугой ORP кривую длины L, охватывающую площадь, большую, чем охватывает данная кривая С, так как включала бы дополнительно площади I и II. Это противоречило бы допущению, что при данной длине L кривая С охватывает наибольшую площадь. Итак, кривая С должна быть выпуклой.

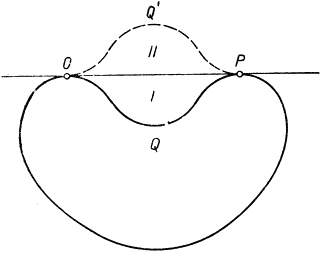
Рис. 226. К доказательству решения изопериметрической проблемы

Возьмем теперь какие-нибудь две точки А, В, которые делят кривую С (являющуюся решением проблемы) на две дуги равной длины. Тогда отрезок АВ разделит область, ограниченную кривой С, на две равновеликие области.

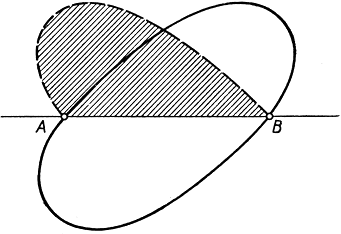
Рис. 227. К доказательству решения изопериметрической проблемы

В самом деле, если бы площади двух областей не были равны, то область большей площади можно было бы отразить относительно А В (рис. 227), и тогда получилась бы замкнутая кривая длины L, охватывающая площадь, большую, чем та, которую охватывает кривая С. Отсюда следует, что любая незамкнутая кривая, представляющая собой половину (по длине) кривой С, является решением следующей проблемы: найти дугу длины -у с конечными точками А и В, охватывающую вместе с отрезком АВ максимальную площадь. Мы покажем теперь, что решением этой новой проблемы является полуокружность, и тогда будет ясно, что решением основной проблемы является окружность. Итак, пусть дуга АОВ есть решение новой проблемы. Достаточно убедиться в том, что всякий вписанный угол, например ∠АОВ (рис. 228), будет прямым: отсюда будет вытекать, что дуга АОВ - полуокружность. Допустим, напротив, что угол ЛОВ не прямой. Заменим тогда треугольник АОВ другим треугольником с теми же сторонами АО я ОВ, но с заключенным между ними углом в 90°; тогда длина дуги АОВ останется та же и притом заштрихованные фигуры не изменятся. Но площадь треугольника АОВ при этом увеличится, так как треугольник с двумя данными сторонами имеет максимальную площадь при условии, что заключенный между ними угол - прямой (см. стр. 363). Итак, новая дуга АОВ (рис. 229) вместе с отрезком АВ охватит большую площадь, чем первоначальная. Полученное противоречие приводит к заключению, что, какова бы ни была точка О на рассматриваемой дуге АВ, угол АОВ должен быть прямым. В таком случае доказательство можно считать законченным: кривая, решающая изопериметрическую проблему, есть окружность.

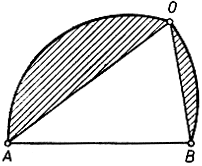
Рис. 228. К доказательству решения изопериметрической проблемы

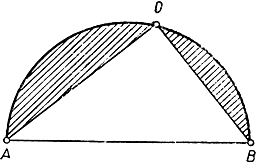
Рис. 229. К доказательству решения изопериметрической проблемы

Изопериметрическое свойство окружности может быть выражено в форме неравенства. Если L есть длина окружности, то охватываемая ею площадь равна 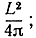поэтому, какова бы ни была замкнутая кривая, непременно оправдывается следующее изопериметрическое неравенство, связывающее длину кривой С и охватываемую ею площадь А:

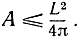
Равенство здесь имеет место только в случае окружности.

^* Как ясно из соображений, приведенных в § 7, доказательство Штейнера имеет лишь условное значение: "Если существует кривая С длины L, охватывающая максимальную площадь, то эта кривая - окружность". Чтобы установить справедливость указанной предпосылки, нужна существенно иная аргументация. Прежде всего установим теорему элементарного содержания: среди всевозможных замкнутых многоугольников Р_n с четным числом сторон 2n и обладающих периметром заданной длины наибольшую площадь имеет правильный 2n-угольник. Доказательство строится по тому же образцу, что и приведенное выше доказательство Штейнера, со следующими изменениями. G вопросом о существовании решения здесь трудностей не возникает: 2n-угольник, а также его периметр и площадь, зависит непрерывно от 4n координат его вершин и, не ограничивая общности, область изменения этих координат (в 4n-мерном пространстве) можно сделать компактной. Таким образом, мы можем смело начинать с утверждения, что некоторый 2n-угольник Р есть решение рассматриваемой теперь проблемы, и затем переходить к анализу его свойств. Как и в штейнеровском доказательстве, доказывается, что многоугольник Р выпуклый. Затем убедимся, что все 2n сторон Р равны между собой. Допустим, напротив, что две смежные стороны АВ и ВС имеют различные длины; тогда можно от многоугольника Р отрезать треугольник ABC и заменить его равнобедренным треугольником АВ'С, в котором АВ' + В'С = АВ + ВС и площадь которого больше (см. § 1). Тогда мы получим многоугольник Р' с тем же периметром, но с большей площадью, вопреки сделанному допущению. Итак, все стороны Р должны быть равны между собой. Остается показать, что многоугольник Р правильный: для этого достаточно убедиться, что около Р можно описать окружность. Доказательство строится дальше, как у Штейнера. Устанавливаем прежде всего, что всякая диагональ, соединяющая противоположные вершины, делит площадь на две равные части. Затем доказываем, что все вершины одного из многоугольников, возникающего при разрезании по диагонали, лежат на одной и той же окружности. Восстановить подробности намеченных доказательств (следующих образцу Штейнера) предоставляем читателю в качестве упражнения.

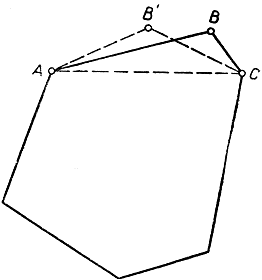
Рис. 230. К доказательству решения изопериметрической проблемы

Существование решения изопериметрической проблемы доказывается с помощью предельного перехода: когда мы увеличиваем неограниченно число сторон 2n многоугольника Р, он в пределе переходит в окружность. Этот же предельный переход дает, очевидно, и само решение.

Рассуждение Штейнера непригодно для доказательства изопериметрического свойства сферы в трехмерном пространстве. Сам Штейнер дал несколько иную, более сложную трактовку этой проблемы, пригодную для пространственного случая, но мы не приводим ее, так как на ее основе трудно получить доказательство существования решения. Вообще доказательство изопериметрического свойства сферы гораздо труднее, чем доказательство соответствующего свойства окружности; в достаточно полном и строгом изложении оно было дано позднее Г. А. Шварцем в работе, чтение которой довольно затруднительно. Свойство, о котором мы говорим, выражается в виде неравенства

где А - площадь замкнутой поверхности, V - охватываемый ею объем; равенство осуществляется лишь для сферы.