4. Трудности, возникающие в более сложных случаях

Если вопрос о существовании экстремума не представляет серьезных затруднений в элементарных проблемах, зависящих от одной, двух и, вообще, конечного числа переменных, то дело обстоит совсем иначе в случае проблемы Дирихле или даже в случае более простых проблем такого же типа. Причина кроется или в том, что область изменения независимого переменного оказывается не компактной, или же в том, что рассматриваемая функция не является непрерывной. В первом примере пункта 2 мы имеем множество путей АО'В, причем О' стремится к A. Все такие пути с точки зрения условия проблемы одинаково допустимы. Но пути АО'В в пределе переходят в прямолинейный отрезок АВ, который сам уже не представляет собой допустимого пути. Множество допустимых путей в этом примере подобно множеству чисел 0<х≤1, для которого не имеет места теорема Вейерштрасса об экстремальных значениях (см. стр. 346). Точно такое же положение вещей и во втором примере: если конусы становятся все тоньше и тоньше, последовательность соответствующих поверхностей в пределе переходит в диск с перпендикуляром, торчащим вверх и заканчивающимся точкой S. Но этот предельный геометрический образ уже не может быть причислен к "допустимым" поверхностям: множество "допустимых" поверхностей и на этот раз не оказывается компактным.

В качестве примера зависимости, не обладающей свойством непрерывности, рассмотрим длину кривой. Длину кривой нельзя считать функцией от конечного числа числовых переменных, так как кривая в целом не может быть охарактеризована конечным числом "координат" и зависимость длины кривой от самой кривой не является непрерывной. Чтобы убедиться в этом, причем О' стремится к A.

соединим две точки А и В, отстоящие одна от другой на расстоянии d, зигзагообразной ломаной Р_n, вместе с отрезком АВ образующей m равносторонних треугольников. Из рис. 225 ясно видно, что длина Р_n при любом n равна в точности 2d Рассмотрим теперь последовательность ломаных линий Р₁, Р₂, ... . Отдельные зигзаги ломаной линии Р_n уменьшаются по своей высоте, в то время как число их увеличивается, и совершенно ясно, что ломаная Р_n в пределе переходит в прямолинейный отрезок А В, в котором уже нет и следов "зигзагообразное". Но длина Р_n все время равна 2d, каково бы ни было n, тогда как длина предельного отрезка АВ равна всего лишь d. Длина кривой, таким образом, не зависит "от самой кривой" непрерывно.

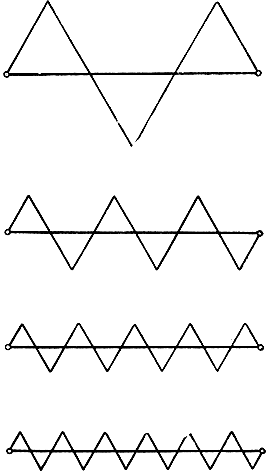
Рис. 225. Приближение отрезка ломаными линиями

Все приведенные примеры подтверждают, что при исследовании вопроса о существовании решения экстремальных проблем в более сложных случаях следует проявлять крайнюю осмотрительность.