3. Экстремальные проблемы элементарного содержания

В задачах элементарного содержания бывает достаточно внимательно проанализировать условия, чтобы уяснить, как обстоит дело с существованием решения. В главе VI, § 5, было исследовано общее понятие компактного множества и было установлено, что непрерывная функция, заданная на некотором множестве элементов, для каких-то элементов множества непременно достигает своих экстремальных значений, если данное множество обладает свойством компактности. В любой из вышеприведенных элементарных проблем сравниваемые между собой числовые элементы могли быть рассматриваемы как значения функции одной или нескольких переменных в области, которая или была компактным множеством, или - без существенного видоизменения проблемы - могла быть сделана таковым. В таких случаях существование максимума или минимума не подлежало сомнению. Остановимся, в качестве примера, на проблеме Штейнера. Рассматриваемая в ней величина есть сумма трех расстояний, и эта последняя зависит от положения точки непрерывно. Хотя область, в которой может двигаться точка, есть вся плоскость, мы можем без ограничения общности провести окружность большого радиуса (включающую весь чертеж) и подчинить точку условию находиться внутри этой окружности или на ней самой. В самом деле, если движущаяся точка будет находиться достаточно далеко от вершин треугольника, сумма трех расстояний от сторон наверное превысит АВ + АС, а последняя величина принадлежит к числу подлежащих сравнению значений нашей функции. Таким образом, если существует минимум для "ограниченной" проблемы (когда точка подчинена дополнительному ограничению), то существует минимум и для неограниченной проблемы. С другой стороны, нетрудно удостовериться, что множество, состоящее из точек внутри круга или на его границе, компактно. Итак, существование минимума в случае проблемы Штейнера доказано.

Насколько существенно свойство компактности области, в которой изменяется независимое переменное, обнаруживает следующий пример. Если заданы две замкнутые кривые С₁ и С₂, то всегда можно найти на С₁ и С₂ соответственно такие две точки Р₁ и Р₂, что расстояние между ними минимально, и две такие точки Q₁ и Q₂, что расстояние между ними максимально. Действительно, расстояние между точкой А₁ на С₁ и точкой А₂ на С₂ есть непрерывная функция, заданная на компактном множестве, элементы которого - пары точек А₁, A₂. Напротив, если данные кривые, не будучи замкнутыми, уходят в бесконечность, проблема может и не иметь решения. На рис. 224 изображены две такие кривые, что ни наименьшее, ни наибольшее расстояния между соответственно принадлежащими им точками не достигаются; при этом нижняя граница расстояний равна нулю, а верхняя граница бесконечна. В иных случаях существует минимум, но не существует максимума. Так, в случае двух ветвей гиперболы (рис. 17, стр. 103) минимальное расстояние реализуется для вершин A и A', тогда как нельзя указать пары точек, между которыми расстояние было бы максимальным.

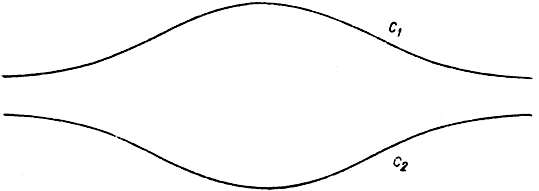
Рис. 224. Кривые, между которыми нет ни наименьшего, ни наибольшего расстояния

Нетрудно понять, чем обусловливается различие между двумя предыдущими примерами; для этого достаточно искусственно ограничить область изменения переменных. Возьмем произвольное положительное число R и подчиним абсциссы точек ограничению |x|≤R. Тогда для обеих проблем будет существовать и минимум, и максимум. Но в первом примере и минимум, и максимум достигаются на границе области, каково бы ни было R, и при неограниченном возрастании R соответствующие точки удаляются в бесконечность. Напротив, во втором примере минимальное расстояние достигается внутри области, и точки, его реализующие, остаются неподвижными, как бы ни возрастало R.