2. Примеры

Проиллюстрируем возникающую трудность двумя примерами.

1) Отметим на прямой L две точки А и В, находящиеся на расстоянии d, и поставим задачу - отыскать ломаную линию кратчайшей длины, которая, выходя из точки А по направлению, перпендикулярному к L, заканчивалась бы в точке В. Так как прямолинейный отрезок АВ безусловно короче всех других путей, связывающих точки A и B, то можно быть уверенным, что любой допустимый (удовлетворяющий требованиям задачи)путь имеет длину, большую, чем d: в самом деле, единственный путь длина которого равна d, есть прямолинейный отрезок АВ, а он не удовлетворяет требованию относительно направления в точке A, т. е. не является допустимым. Рассмотрим, с другой стороны, допустимый путь АОВ на рис. 222. Заменяя точку О точкой О', расположенной ближе к A, мы можем получить новый допустимый путь, длина которого как угодно мало отличается от d; значит, если существует кратчайший допустимый путь, то длина его не может быть больше, чем d, и, следовательно, должна быть в точности равна d. Но мы видели, что единственный путь, имеющий такую длину, не является допустимым. Итак, кратчайшего допустимого пути не существует, и задача наша не имеет решения.

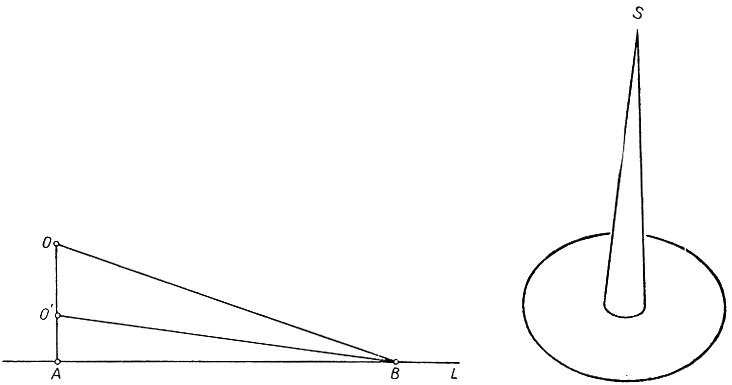
Рис. 222-223. К вопросу о существовании минимума

2) Пусть С - некоторый круг, а S - точка, лежащая выше его центра на расстоянии 1 (рис. 223). Рассмотрим множество поверхностей, ограниченных окружностью С и проходящих через точку S, притом лежащих "над" кругом С (в том смысле, что никакие две различные точки этой поверхности не могут вертикально проектироваться в одну и ту же точку круга С). Какая поверхность из рассматриваемого множества обладает наименьшей площадью? Каким бы естественным ни казался этот вопрос, положительного ответа на него дать нельзя: допустимой поверхности с наименьшей площадью не существует. Если бы поверхность не была подчинена условию проходить через точку S, тогда решением задачи был бы, очевидно", плоский диск, ограниченный окружностью С. Обозначим площадь этого диска через А. Всякая другая поверхность, ограниченная окружностью С, непременно имеет площадь, большую, чем А. Но можно указать допустимую поверхность, площадь которой будет отличаться от А как угодно мало. В самом деле, возьмем коническую поверхность высоты, равной 1 - такую "тоненькую", чтобы ее площадь была меньше заранее назначенного маленького числа. Поместим эту поверхность посреди диска так, чтобы ее вершина попала в точку S, и затем рассмотрим поверхность, образованную из нашей конической поверхности и той части диска, которая окажется вне основания конуса. Совершенно ясно, что построенная таким образом поверхность, только вблизи центра диска отличающаяся от самого диска, обладает площадью, превосходящей А меньше чем на заранее назначенное число. Так как это последнее число может быть выбрано сколь угодно малым, то отсюда следует, что минимум площади (если он существует) не может отличаться от площади диска А. Но среди поверхностей, ограниченных контуром С, только сам диск обладает площадью А; однако диск не проходит через точку S и, значит, не является допустимой поверхностью; следовательно, решения задачи не существует.

Мы можем избавить себя от труда приводить дальнейшие относящиеся сюда софистически утонченные примеры, указанные Вейерштрассом. Уже приведенные примеры достаточно убедительно показывают, что существование минимума не является тривиальным моментом в математическом доказательстве. Попробуем взглянуть на рассматриваемый вопрос с более отвлеченной точки зрения. Представим себе некоторый определенный класс объектов, например кривых или поверхностей; пусть каждому объекту этого класса поставлено в соответствие - как функция этого объекта - некоторое число, например длина или площадь. Если в классе содержится лишь конечное число объектов, то среди соответствующих чисел неизбежно имеется наибольшее и наименьшее. Но если в классе содержится бесконечное множество объектов, то даже в том случае, если все соответствующие числа заключены между двумя конечными границами, среди них вовсе не обязательно найдется наибольшее и наименьшее. На числовой оси множество чисел изображается в виде множества точек. Предположим, ограничившись простейшим случаем, что все числа множества положительные. Такое множество непременно имеет "нижнюю границу" - такое число а, меньше которого в нашем множестве нет ни одного числа и которое или само есть элемент множества, или как угодно мало отличается от некоторого элемента множества. Если а само принадлежит множеству, то оно является его наименьшим элементом; в противном случае множество не содержит вовсе наименьшего элемента. Например, множество чисел 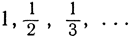не содержит наименьшего элемента, так как нижняя граница 0 не принадлежит множеству. Такого рода отвлеченные примеры иллюстрируют логические трудности, связанные с проблемой существования. Математическое решение минимальной проблемы нельзя назвать исчерпывающим, если в явной или в неявной форме не устанавливается, что среди элементов числового множества, рассматриваемого в связи с проблемой, существует наименьший.